第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
24. (12 分) 小明思考解决如下问题:
原题:如图,$\angle A = 36^{\circ}$,$B$,$C$ 分别是射线 $AN$,$AM$ 上的动点,以 $BC$ 为腰在 $\triangle ABC$ 的外侧作等腰 $\triangle BCD$,使 $\angle CBD = 108^{\circ}$,过点 $D$ 作 $DE \perp AN$ 于点 $E$,交射线 $AM$ 于点 $F$,过点 $D$ 作 $DG // AN$ 交 $AM$ 于点 $G$,探究线段 $AC$ 与 $GF$ 的数量关系。
小明与同桌讨论后,进行如下解答:
(1) 特殊情况,探索结论
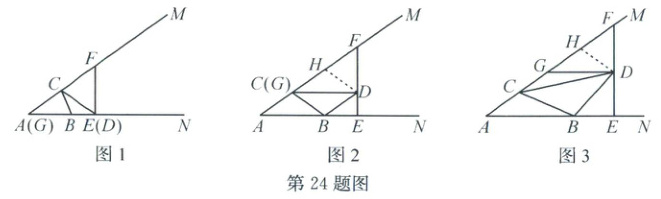
① 如图 1,当点 $G$ 与点 $A$ 重合时,点 $D$ 与点 $E$ 重合,小明探索得 $GF = 2AC$,请你证明。(4 分)
② 如图 2,当点 $G$ 与点 $C$ 重合时,小明取 $GF$ 的中点 $H$,连结 $DH$,探究得到线段 $AC$ 与 $GF$ 的数量关系,请你完善小明的探究过程。(4 分)
(2) 特例启发,解答题目
解:如图 3,取 $GF$ 的中点 $H$,连结 $DH$(请完成后续解答过程)。(4 分)
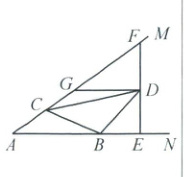
原题:如图,$\angle A = 36^{\circ}$,$B$,$C$ 分别是射线 $AN$,$AM$ 上的动点,以 $BC$ 为腰在 $\triangle ABC$ 的外侧作等腰 $\triangle BCD$,使 $\angle CBD = 108^{\circ}$,过点 $D$ 作 $DE \perp AN$ 于点 $E$,交射线 $AM$ 于点 $F$,过点 $D$ 作 $DG // AN$ 交 $AM$ 于点 $G$,探究线段 $AC$ 与 $GF$ 的数量关系。
小明与同桌讨论后,进行如下解答:
(1) 特殊情况,探索结论
① 如图 1,当点 $G$ 与点 $A$ 重合时,点 $D$ 与点 $E$ 重合,小明探索得 $GF = 2AC$,请你证明。(4 分)
② 如图 2,当点 $G$ 与点 $C$ 重合时,小明取 $GF$ 的中点 $H$,连结 $DH$,探究得到线段 $AC$ 与 $GF$ 的数量关系,请你完善小明的探究过程。(4 分)
(2) 特例启发,解答题目
解:如图 3,取 $GF$ 的中点 $H$,连结 $DH$(请完成后续解答过程)。(4 分)


答案:
24.解:
(1)①证明:在等腰$\triangle BCD$中,$\angle CBD = 108^{\circ}$,所以$\angle BDC = \angle BCD = 36^{\circ} = \angle A$。所以$AC = CD$。因为$DF\perp AN$,所以$\angle ADF = 90^{\circ}$。因为$\angle A = 36^{\circ}$,所以$\angle AFD = \angle CDF = 54^{\circ}$。所以$CD = CF$。所以$GF=AC + CF = 2AC$。
②因为$DF\perp AN$,$CD//AN$,H是GF的中点,所以$DF\perp CD$,所以$GF = 2HD$,$CH = HD$。因为$CD//AN$,$CB = BD$,$\angle CBD = 108^{\circ}$,所以$\angle HCD = \angle A = \angle CDB = \angle DCB = \angle HDC = \angle CBA = 36^{\circ}$。又$CD = CD$,所以$\triangle CHD\cong\triangle CBD(ASA)$。所以$HD = BD = BC$。所以$AC = BC = HD$。所以$GF = 2AC$。
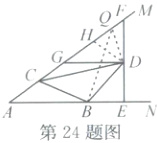
(2)$GF = 2AC$,理由如下:如图,在射线AM上取点Q,使$BA = BQ$,连结DQ。因为$BA = BQ$,$\angle A = 36^{\circ}$,所以$\angle BQA = \angle A = 36^{\circ}$,所以$\angle ABQ = 180^{\circ} - 2×36^{\circ} = 108^{\circ}$,所以$\angle ABQ - \angle CBQ = \angle CBD - \angle CBQ$,即$\angle ABC = \angle QBD$。因为$CB = BD$,所以$\triangle BAC\cong\triangle BQD(SAS)$。所以$AC = QD$,$\angle BQD = \angle A = 36^{\circ}$,所以$\angle HQD = \angle AQB + \angle BQD = 72^{\circ}$。因为$GD//AN$,$DF\perp AN$,所以$\angle QGD = \angle A = 36^{\circ}$,$\angle GDF = \angle AEF = 90^{\circ}$。因为H是GF的中点,所以$GF = 2GH = 2HD$。所以$\angle HGD = \angle HDG = 36^{\circ}$,所以$\angle QHD = \angle HGD + \angle HDG = 72^{\circ}$。所以$\angle QHD = \angle HQD$。所以$HD = QD = AC$。所以$GF = 2AC$。
24.解:
(1)①证明:在等腰$\triangle BCD$中,$\angle CBD = 108^{\circ}$,所以$\angle BDC = \angle BCD = 36^{\circ} = \angle A$。所以$AC = CD$。因为$DF\perp AN$,所以$\angle ADF = 90^{\circ}$。因为$\angle A = 36^{\circ}$,所以$\angle AFD = \angle CDF = 54^{\circ}$。所以$CD = CF$。所以$GF=AC + CF = 2AC$。

②因为$DF\perp AN$,$CD//AN$,H是GF的中点,所以$DF\perp CD$,所以$GF = 2HD$,$CH = HD$。因为$CD//AN$,$CB = BD$,$\angle CBD = 108^{\circ}$,所以$\angle HCD = \angle A = \angle CDB = \angle DCB = \angle HDC = \angle CBA = 36^{\circ}$。又$CD = CD$,所以$\triangle CHD\cong\triangle CBD(ASA)$。所以$HD = BD = BC$。所以$AC = BC = HD$。所以$GF = 2AC$。
(2)$GF = 2AC$,理由如下:如图,在射线AM上取点Q,使$BA = BQ$,连结DQ。因为$BA = BQ$,$\angle A = 36^{\circ}$,所以$\angle BQA = \angle A = 36^{\circ}$,所以$\angle ABQ = 180^{\circ} - 2×36^{\circ} = 108^{\circ}$,所以$\angle ABQ - \angle CBQ = \angle CBD - \angle CBQ$,即$\angle ABC = \angle QBD$。因为$CB = BD$,所以$\triangle BAC\cong\triangle BQD(SAS)$。所以$AC = QD$,$\angle BQD = \angle A = 36^{\circ}$,所以$\angle HQD = \angle AQB + \angle BQD = 72^{\circ}$。因为$GD//AN$,$DF\perp AN$,所以$\angle QGD = \angle A = 36^{\circ}$,$\angle GDF = \angle AEF = 90^{\circ}$。因为H是GF的中点,所以$GF = 2GH = 2HD$。所以$\angle HGD = \angle HDG = 36^{\circ}$,所以$\angle QHD = \angle HGD + \angle HDG = 72^{\circ}$。所以$\angle QHD = \angle HQD$。所以$HD = QD = AC$。所以$GF = 2AC$。
查看更多完整答案,请扫码查看


