《2025年期末直通车八年级数学上册人教版》

7. 如图，在 $\triangle ABC$ 和 $\triangle ADC$ 中，$AB = AD$，若添加条件 $\angle ABC = \angle ADC = 90^{\circ}$ 来判定 $\triangle ABC \cong \triangle ADC$，其判定依据是(C)

A.SSS
B.ASA
C.HL
D.AAS

答案： 7.C

8. 下列命题是假命题的是(D)

A.对顶角相等
B.若 $ac^{2} ＞ bc^{2}$，则 $a ＞ b$
C.全等三角形的对应边相等
D.若 $|a| = |b|$，则 $a = b$

答案： 8.D

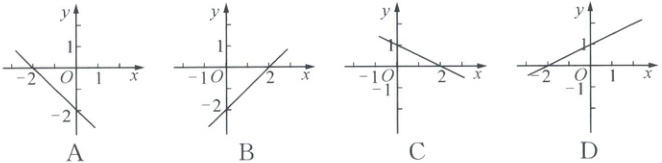
9. 已知不等式 $kx + b ＞ 0$ 的解是 $x ＞ 2$，则一次函数 $y = kx + b$ 的图象大致是(B)

答案： 9.B

10. 赵爽是我国著名的数学家，“赵爽弦图”是他研究勾股定理的重要成果。古人有记载“勾三，股四，则弦五”的定理。如图，以三边长分别为 3，4，5 的四个直角三角形拼成一个正方形 $ABCD$，以 $BH$ 为边再作一个正方形 $BH IJ$，连结 $CH$，$DH$，$DI$，则 $\triangle CDH$ 的面积为(C)

A.$\frac{15}{2}$
B.7
C.$\frac{13}{2}$
D.$\frac{11}{2}$

答案： 10.C 解析：$S_{\triangle CDH}=S_{五边形EHDIC}-S_{\triangle EHC}-S_{\triangle CID}=S_{四边形EHIC}+S_{\triangle HDI}-S_{\triangle EHC}-S_{\triangle CID}=4×1×\frac{1}{2}+\frac{1}{2}×4×3-\frac{1}{2}×1×3=\frac{13}{2}$。 故选C。

11. 函数 $y = \frac{1}{2x - 5}$ 中自变量 $x$ 的取值范围是$x\neq\frac{5}{2}$。

答案： 11.$x\neq\frac{5}{2}$

12. “3 与 $a$ 的和是正数”用不等式表示为$3 + a ＞ 0$。

答案： 12.$3 + a ＞ 0$

13. 一次函数 $y = 2x + 1$ 图象上有两点 $(2,y_{1})$，$(-1,y_{2})$，则 $y_{1}$$＞ $(填“$＞$”“$＜$”或“$=$”)$y_{2}$。

答案： 13.$＞ $

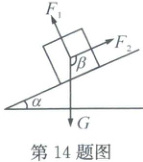
14. 一个箱子静止放在斜坡上，其受力分析如图所示，重力 $G$ 的方向竖直向下，支持力 $F_{1}$ 的方向与斜面垂直，摩擦力 $F_{2}$ 的方向与斜面平行。若摩擦力 $F_{2}$ 与重力 $G$ 方向的夹角 $\beta$ 的度数为 $113^{\circ}$，则图中角 $\alpha$ 的度数为$23^{\circ}$。

答案： 14.$23^{\circ}$