《2025年期末直通车八年级数学上册人教版》

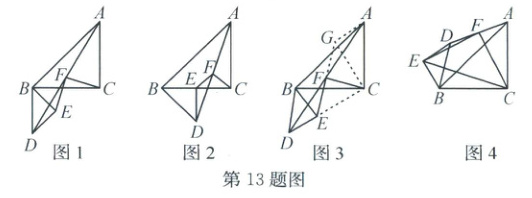
13.(2024·舟山定海)小王同学在学习完第2章《特殊三角形》后，剪了两张等腰直角三角形纸片，并将锐角顶点叠合放置成如图1所示图形，其中$\angle ACB = \angle BED = 90^{\circ}$，$CA = CB$，$EB = ED$，连结$AD$后取中点$F$，再连结$FE$和$FC$。探究$FE$与$FC$的位置及数量关系。
(1)小王同学变化等腰$Rt\triangle BDE$的位置，使得点$E$落在$BC$上，如图2所示，请猜想$EF$与$CF$的位置及数量关系分别是EF⊥CF，EF=CF。
(2)小王同学思考：“在一般位置时，(1)中猜想的结论是否仍成立，能否给出证明？”他带着问题与同学展开合作交流，最后得到这样的证明方案：如图3所示，过点$A$作$DE$的平行线交$EF$的延长线于点$G$，连结$CG$，$EC$，…，请根据以上思路完成猜想的证明。
(3)小王同学继续变化等腰$Rt\triangle BDE$的位置，如图4所示，点$E$在$BC$所在直线的上方，且$\angle EBC = 120^{\circ}$。若$BC = 4$，$ED = 2$，请利用猜想的结论求出$\triangle EFC$的面积。

答案：
13.
(1)EF⊥CF　EF=CF　
(2)证明:在△AGF和△DEF中，因为AG//DE,所以∠AGF=∠DEF,∠AFG=∠DFE。又因为AF=DF,所以△AGF≌△DEF(AAS)。所以DE=AG =BE,∠GAC=∠EDF+∠FAC=45°−∠BDA+∠FAC=
45°−∠BDA+45°−∠BAD=90°−(∠BDA+∠BAD),∠CBE=180°−∠ABC−∠DBE−∠BDA−∠BAD=90°−(∠BDA+∠BAD),所以∠EBC=∠GAC。又因为BC=
AC,所以△EBC≌△GAC(SAS)。所以EC=GC,∠ACG=
∠BCE。因为∠BCG公共角，所以∠ACB=∠ACG+∠GCB=∠GCB+∠BCE=90°,所以△GCE是等腰直角三角形。因为F为GE中点，所以易得CF⊥
FE,FE=CF。　
(3)解:如图,过点E作
EN⊥CB的延长线于点N。因为∠EBC
　　　　　　　　　　　　　　　　 =120°,所以∠EBN=60°,易知BN=
$\frac{1}{2}$BE=1,所以EN= $\sqrt{2²−1²}$=$\sqrt{3}$。在
Rt△NCE中,EN²+(NB+BC)²=EC²,所以EC= $\sqrt{28}$
因为△EFC为等腰直角三角形,∠EFC=90°,所以EF²+
CF²=EC²,所以EF=FC= $\sqrt{14}$,所以S_{△EFC}=$\frac{1}{2}$×EF×FC=$\frac{1}{2}$×14=7。