《2025年期末直通车八年级数学上册人教版》

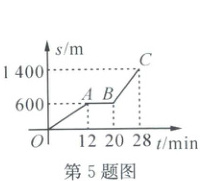
5. (2024·杭州西湖)如图,图中的折线$ OABC $反映了圆圆从家到学校所走的路程$ s $(m)与时间$ t $(min)的函数关系,其中,$ OA $所在直线的表达式为$ y = k _ { 1 } x ( k _ { 1 } \neq 0 ) $,$ BC $所在直线的表达式为$ y = k _ { 2 } x + b ( k _ { 2 } \neq 0 ) $,则$ k _ { 2 } - k _ { 1 } = $50。

答案： 5.50

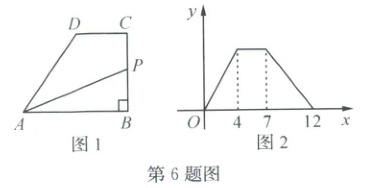
6. (2024·新昌)如图1,在四边形$ ABCD $中,$ AB // CD $,$ AB \perp BC $,动点$ P $从点$ B $出发,沿$ B \to C \to D \to A $的方向运动,到达点$ A $停止。设点$ P $的运动路程为$ x $,$ \triangle ABP $的面积为$ y $,如果$ y $与$ x $的函数图象如图2所示,那么$ AB $边的长度为6。

答案：
6.6解析:如图，过点$D$作$DH\perp AB$于点$H$。所以$\angle DHB=\angle DHA = 90^{\circ}$。又因为$AB\perp BC$，$AB// CD$，所以四边形$DHBC$是矩形，所以$DH = BC = 4$，$HB = CD = 3$，所以$AH=\sqrt{AD^{2}-DH^{2}} = 3$，所以$AB = AH + HB = 6$。

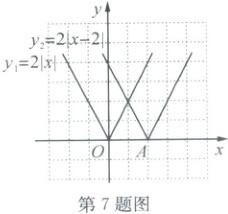
7. (2024·湖州吴兴)图象法是函数的表示方法之一,下面我们就一类特殊的函数图象展开探究。

(1)函数$ y _ { 3 } = 2 | x - 2 | + 3 $的最小值为3。
(2)函数$ y _ { 4 } = 2 | x - m | + 3 $在$ - 2 \leq x \leq 1 $中有最小值4,则$ m $的值是$\frac{3}{2}$或$-\frac{5}{2}$。

答案： 7.
(1)$3$
(2)$\frac{3}{2}$或$-\frac{5}{2}$解析:
(1)因为$2|x - 2|\geqslant0$，所以$2|x - 2|+3\geqslant3$，所以函数$y=2|x - 2|+3$的最小值是$3$。
(2)函数$y=2|x - m|+3$的图象的对称轴是直线$x = m$。①若$m＞1$，因为函数$y=2|x - m|+3$在$-2\leqslant x\leqslant1$中有最小值$4$，即$x = 1$时，$y = 4$，所以$4 = 2|1 - m|+3$，解得$m=\frac{3}{2}$或$\frac{1}{2}$(舍去)；②若$m＜-2$，因为函数$y=2|x - m|+3$在$-2\leqslant x\leqslant1$中有最小值$4$，即$x = -2$时$y = 4$，所以$4 = 2|-2 - m|+3$，解得$m=-\frac{5}{2}$或$m=-\frac{3}{2}$(舍去)；③若$-2\leqslant m\leqslant1$，则易知此时$y$的最小值为$3$，与题意不符，故舍去。综上，$m$的值为$\frac{3}{2}$或$-\frac{5}{2}$。

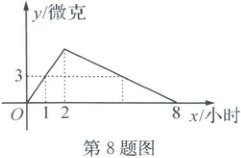
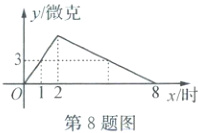
8. (2025·嵊州)某医药研究所研发了一种新药,在实验药效时发现,如果按规定剂量服用,每毫升血液中含药量$ y $(微克)随时间$ x $(小时)的变化情况如图所示,那么当按规定剂量服药后,根据图象回答下列问题:
(1)当$ x \leq 2 $时,求$ y $关于$ x $的函数关系式。
(2)当$ 2 \leq x \leq 8 $时,求$ y $关于$ x $的函数关系式。
(3)如果每毫升血液中含药量为3微克或3微克以上时治疗疾病最有效,求这个有效时间的范围。

答案：
8.解:
(1)当$x\leqslant2$时，设$y = kx$，把$(1,3)$代入解得$k = 3$，故函数关系式为$y = 3x$。
(2)当$2\leqslant x\leqslant8$时，设$y = k'x + b$，由
(1)，易得交点坐标为$(2,6)$，

把$(2,6)$和$(8,0)$代入，解得$\begin{cases}k'=-1\\b = 8\end{cases}$，故函数关系式为$y=-x + 8$。
(3)当$y = 3$时，$-x + 8 = 3$，$x = 5$，有效时间范围为$1\leqslant x\leqslant5$。