《2025年期末直通车八年级数学上册人教版》

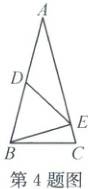
4.(2025·杭州滨江)如图，在△ABC中，AB=AC=2BC=4，D为AB中点，点E在AC上，且DE=AD，则CE的长为$\frac{1}{2}$。

答案： 4.$\frac{1}{2}$

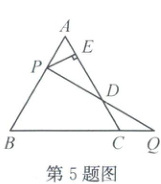
5.(2024·绍兴上虞)如图，已知等边△ABC的边长为4，过AB边上一点P作PE⊥AC于点E，Q是BC延长线上一点，且CQ=PA，连结PQ交AC于点D，则DE的长为2。

答案： 5.2

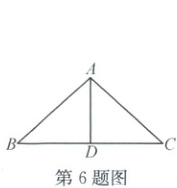
6.(2023·丽水莲都)如图，AD是△ABC的BC边上的中线，AB=7，AD=5，则AC的取值范围是3＜AC＜17。

答案：
6.3＜AC＜17　解析：如图，延长AD至点E，使得DE=AD=5，连结CE。因为AD为△ABC的BC边上的中线，所以BD=CD。在△ABD和△ECD中，AD=ED，∠ADB=∠EDC，BD=CD，所以△ABD≌△ECD(SAS)，所以CE=AB=7。在△ACE中，AE - EC＜AC＜AE + EC，即5 + 5 - 7＜AC＜5 + 5 + 7，所以3＜AC＜17。

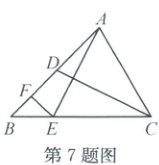
7.(2024·长兴)如图，已知在△ABC中，点D，E分别在边AB，BC上，过点E作EF⊥AB于点F，∠B=∠EAF+∠BCD，AE=CD，若BF=6，则AD的长为12。

答案：
7.12　解析：设∠BAE=∠1，∠BCD=∠2。如图，在AF上取一点T，使FT=FB，连结ET。在BC上取一点N，使CN=ET，连结DN。因为∠BFE=∠TFE=90°，FE=FE，所以△BFE≌△TFE(SAS)，所以∠FTE=∠B=∠1 + ∠2=∠1 + ∠AET，所以∠2=∠AET。因为EA=CD，所以△ATE≌△DNC(SAS)。所以AT=DN。又∠DNB=∠2 + ∠CDN=∠1 + ∠2，所以BD=DN，所以AT=BD，所以AD=BT=2BF =12。

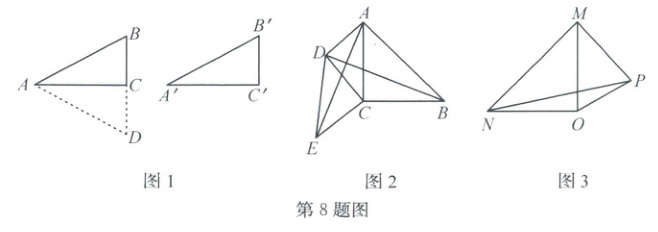
8.（2025·嵊州）综合与实践：小嵊与小州两个同学在学习了“直角三角形全等的判定”后，对数学中重要的学习方法“构造法”展开了课后探究。
【情景再现】
已知，如图1，在△ACB和△A'C'B'中，∠C=∠C'=90°，AB=A'B'，AC=A'C'。
下面是用“构造法”证明两个直角三角形全等的部分过程。
证明：如图1，延长BC至D，使CD=B'C'，连结AD。
因为AC=A'C'（已知），∠ACD=90°=∠C'，
所以△ADC≌△A'B'C'（SAS），
所以AD=A'B'（全等三角形的对应边相等）。
……
所以△ABC≌△ADC（SSS）。
所以△ABC≌△A'B'C'。
【实践解决】
（1）请结合“情景再现”的证明过程，把“……”的部分补充完整。
（2）小嵊进行了如下的思考：如图2，△ABC和△DCE都是等腰直角三角形，且∠ACB=∠DCE=90°。连结AD，若AC=2，AD=1，∠DAC=45°，求AE的长。
（3）小州结合“构造法”进行进一步探究：如图3，△MON是等腰直角三角形，∠MON=90°，P是△MON外一点，∠MPO=75°，PO=2，MP=2$\sqrt{2}$，求线段NP的长。

答案：
8.
(1)证明：因为AB=A'B'，所以AB=AD。因为∠ACB=90°，所以CD=BC。
(2)解：因为△ABC和△DCE都是等腰直角三角形，所以AC=BC=2，CD=CE，∠ACB=∠DCE=90°。所以∠CAB=45°，AB=$\sqrt{AC^{2}+BC^{2}}=2\sqrt{2}$。因为∠ACB=∠DCE，所以∠ACB + ∠ACD=∠DCE + ∠ACD，即∠BCD=∠ACE。在△BCD和△ACE中，$\begin{cases}BC=AC\\∠BCD=∠ACE\\CD=CE\end{cases}$所以△BCD≌△ACE。所以BD=AE。因为∠DAC=45°，所以∠BAD=90°。所以BD=$\sqrt{AB^{2}+AD^{2}}=3$。所以AE=3。
(3)解：如图，构造等腰三角形OPE，使得∠POE=90°，PO=EO。连结ME，与
(2)中同理可证△PON≌△EOM，所以NP=ME。因为∠POE=90°，PO=EO=2，所以∠OPE=45°，PE=$\sqrt{OP^{2}+OE^{2}}=2\sqrt{2}$。所以NP=PE=$2\sqrt{2}$。因为∠MPO=75°，所以∠MPE=120°。所以ME=$2\sqrt{6}$。所以NP=$2\sqrt{6}$。