《2025年期末直通车八年级数学上册人教版》

24. (12 分)综合与实践
【建立模型】
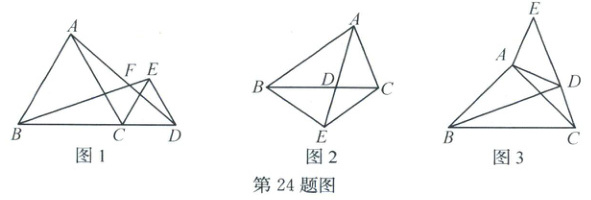
(1) 如图 1,$ \triangle ABC $ 为等边三角形,点 $ D $ 在 $ BC $ 的延长线上,在 $ BD $ 的同侧以 $ CD $ 为边构造等边三角形 $ CDE $,连结 $ BE $,$ AD $ 交于点 $ F $。求证:$ BE = AD $,并直接写出 $ \angle AFB $ 的度数。(4 分)
【应用模型】
(2) ① 如图 2,在 $ \triangle ABC $ 中,$ AD $ 平分 $ \angle BAC $,且 $ AD = AC $,点 $ E $ 在 $ AD $ 的延长线上,且 $ AB = AE $,连结 $ BE $,$ CE $,求证:$ BE = CE $。(4 分)
② 如图 3,$ \triangle ABC $ 和 $ \triangle ADE $ 都是等腰三角形,$ \angle BAC = \angle DAE = 90^{\circ} $,点 $ C $ 恰好在 $ ED $ 延长线上,连结 $ BD $,若 $ AB = 4 $,$ AE = 2 $,求 $ \triangle BDC $ 的面积。(4 分)

答案： 24.
(1)证明：因为$\triangle ABC$，$\triangle CDE$均为等边三角形，所以$BC = AC$，$\angle BCA=\angle ECD = 60^{\circ}$，$CE = CD$。所以$\angle BCE=\angle ACD$，所以$\triangle BCE \cong \triangle ACD(SAS)$。所以$BE = AD$，$\angle AFB = 60^{\circ}$。
(2)①证明：因为$AB = AE$，$\angle BAD=\angle EAC$，$AD = AC$，所以$\triangle ABD \cong \triangle AEC$，所以$BD = EC$。又因为$\angle BED=\frac{180^{\circ}-\angle BAE}{2}$，$\angle BDE=\frac{180^{\circ}-\angle DAC}{2}$，$\angle BAE=\angle DAC$，所以$\angle BED=\angle BDE$，所以$BD = BE$，故$BE = CE$。
②解：易证$\triangle BAD \cong \triangle CAE$，则$BD = CE$，$\angle ABD=\angle ACE$。所以$\angle BDC = 180^{\circ}-\angle DBC-\angle BCD = 180^{\circ}-\angle DBC-\angle ACB-\angle ACE = 180^{\circ}-\angle DBC-\angle ABD-\angle ACB = 90^{\circ}$，即$\triangle BDC$是直角三角形。由题易得$DE = 2\sqrt{2}$，$BC = 4\sqrt{2}$，设$CD = x$，则$BD = CE = x + 2\sqrt{2}$，所以在$Rt\triangle BDC$中，有$(x + 2\sqrt{2})^{2}+x^{2}=32$，故$S_{\triangle BDC}=\frac{1}{2}CD · BD=\frac{1}{2}x · (x + 2\sqrt{2})=\frac{1}{4}[(x + 2\sqrt{2})^{2}+x^{2}-(x + 2\sqrt{2}-x)^{2}]=\frac{1}{4} × (32 - 8)=6$。