《2025年期末直通车八年级数学上册人教版》

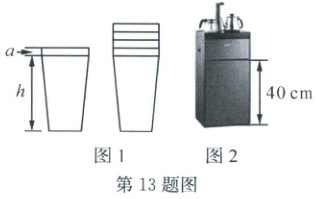
13.(2024·杭州拱墅)图 1 是 1 个纸杯和 4 个叠放在一起的纸杯的示意图，为了建立一个函数探究叠在一起的杯子的总高度 $ y $($ cm $)随着杯子数量 $ x $(个)的变化规律，设杯子底部到杯沿底边高为 $ h $($ cm $)，杯沿高为 $ a $($ cm $)。
(1) 杯子底部到杯沿底边高 $ h $ 为常量，杯沿高 $ a $ 为常量。(均填“常量”或“变量”)
(2) 杯子的总高度 $ y $ 是杯子数量 $ x $ 的函数，可建立函数表示它们的关系为 $ y = $$h + ax$(用 $ x $，$ a $，$ h $ 表示)。
(3) ①某型号的 1 个纸杯总高度为 9.1 cm，4 个叠在一起的纸杯总高度为 10.9 cm，求 $ h $ 和 $ a $ 的值。
②图 2 是某品牌饮水机的示意图，储藏柜的高度是 40 cm。若要将①中该型号纸杯叠放后竖直(杯口向上)放入储藏柜，最多能将多少个纸杯叠放在一起？

答案： 13.
(1)常量 常量
(2)$h + ax$
(3)①解：由题意，得
$\begin{cases}h + a = 9.1,\\h + 4a = 10.9.\end{cases}$解得$\begin{cases}h = 8.5,\\a = 0.6.\end{cases}$②解：由题意，得$8.5 + 0.6x\leq40$，解得$x\leq52.5$。因为$x$是整数，所以最多能将52个纸杯叠放在一起。