《2025年期末直通车八年级数学上册人教版》

22. (10 分)综合与实践
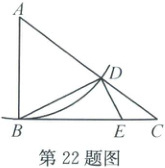
如图,在 $ \triangle ABC $ 中,$ \angle ABC = 90^{\circ} $。以点 $ A $ 为圆心,$ AB $ 为半径画弧,交 $ AC $ 于点 $ D $,连结 $ BD $。过点 $ D $ 作 $ BD $ 的垂线,交 $ BC $ 于点 $ E $。观察这个图形,同学们纷纷提出自己的想法。
(1)圆圆说:“$ \angle DBE = \angle CDE $。”你认为圆圆的说法正确? 请说明理由。(4 分)
(2)方方说:“若 $ BD = 2DE $,则 $ BE = AD $。”请你证明结论。(4 分)
(3)小明说:“给出条件 $ BE = 2CD $,就可以确定 $ \angle A $ 的度数。”请你直接写出 $ \angle A $ 的度数。(2 分)

答案：
22.
(1)解：圆圆的说法正确。理由如下：由题意，得AB = AD，∠BDE = 90°。因为AB = AD，所以∠ABD = ∠ADB。因为∠ABD + ∠DBE = 90°，∠ADB + ∠CDE = 90°，所以∠DBE = ∠CDE。所以圆圆的说法正确。
(2)解：如图，过点A作AH⊥BD，垂足为点H。因为AB = AD，AH⊥BD，所以BH = HD。又因为BD = 2DE，所以BH = DE。因为∠ABD + ∠DBE = 90°，∠ABD + ∠BAH = 90°，所以∠BAH = ∠DBE。又因为∠BHA = ∠BED = 90°，所以△ABH≌△BED，所以BE = AB，所以BE = AD。
(3)∠A = 45°。

23. (10 分)在直角坐标系中,点 $ A(m,0) $ 在函数 $ y_1 = ax + 2a - 1 \left( a \neq 0 且 a \neq \frac{1}{2} \right) $ 的图象上。
(1)若 $ m = 3 $,求 $ a $ 的值。(3 分)
(2)若 $ 2 ＜ m ＜ 3 $,求 $ a $ 的取值范围。(3 分)
(3)设函数 $ y_2 = \frac{1}{2}x $,若 $ a ＜ 0 $,当 $ y_1 ＜ y_2 $ 时,求 $ x $ 的取值范围。(4 分)

答案： 23.解：
(1)把点A(3,0)代入直线$y_{1}$，可得0 = 3a + 2a - 1，所以a = $\frac{1}{5}$。
(2)把点A(m,0)代入直线$y_{1}$，可得0 = ma + 2a - 1，(m + 2)a = 1。因为2＜m＜3，所以4＜m + 2＜5，所以$\frac{1}{5}$＜a＜$\frac{1}{4}$。
(3)方法1：联立$y_{1}=ax + 2a - 1$，$y_{2}=\frac{1}{2}x$，可得$\frac{1}{2}x=ax + 2a - 1$，所以$(a - \frac{1}{2})(x + 2)=0$。因为a≠0且a≠$\frac{1}{2}$，所以x = - 2。因为a＜0，所以当$y_{1}$＜$y_{2}$时，x ＞ - 2。
方法2：因为$y_{1}=ax + 2a - 1=a(x + 2)-1$，所以$y_{1}$图象过点(-2,-1)。因为x = - 2时，$y_{2}=-1$，所以点(-2,-1)也在$y_{2}=\frac{1}{2}x$的图象上，$y_{1}=ax + 2a - 1$与$y_{2}=\frac{1}{2}x$图象的交点是(-2,-1)。因为a＜0，$y_{1}$随x的增大而减小，$\frac{1}{2}$＞0，$y_{2}$随x的增大而增大，所以当$y_{1}$＜$y_{2}$时，x ＞ - 2。