《2025年期末直通车八年级数学上册人教版》

20. (8 分)已知一次函数 $ y = (a + 1)x + a - 2 $ ($ a $ 为常数,$ a \neq - 1 $)的图象过点$ (-2,4) $。
(1) 求一次函数的表达式。(3 分)
(2) 若点 $ P(m,y_{1}) $,$ Q(m + 1,y_{2}) $ 都在该函数的图象上。
① 当 $ - 1 ＜ m ＜ 2 $ 时,求 $ y_{1} $ 的取值范围。(2 分)
② 请判断 $ y_{1} $,$ y_{2} $ 的大小关系,并说明理由。(3 分)

答案： 20.解：
(1)把(-2,4)代入$y=(a + 1)x + a - 2$，得$-2(a + 1)+a - 2 = 4$，解得$a = -8$。故一次函数的表达式为$y = -7x - 10$。
(2)①因为$-1＜m＜2$，所以由$y_{1}=-7m - 10$，得$-24＜y_{1}＜-3$。②因为$-7＜0$，$m＜m + 1$，所以$y_{1}＞y_{2}$。

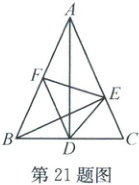
21. (8 分)如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ AD $ 为 $ BC $ 上的中线,$ BE \perp AC $,垂足为点 $ E $,$ F $ 为 $ AB $ 的中点,连结 $ EF $,$ FD $,$ DE $。
(1) 求证:$ EF = FD $。
(2) 已知 $ \angle BAC = 50^{\circ} $,求 $ \angle FED $ 的度数。

答案： 21.
(1)证明：因为$BE \perp AC$，$AD \perp BC$（由$AB = AC$，$BD = CD$易得），F为AB中点，所以$FD=\frac{1}{2}AB = EF$。
(2)解：因为$\angle BAC = 50^{\circ}$，所以$\angle ABE = 40^{\circ}$。又因为$BF = FE$，$BD = DE$，所以易证$FD \perp BE$，所以$\angle EFD=\angle BFD = 50^{\circ}$，所以在$\triangle FDE$中，$\angle FED=\angle FDE=\frac{180^{\circ}-\angle EFD}{2}=65^{\circ}$。

22. (10 分)某校开设了内容丰富的社团活动,其中“编织中国结”社团为布置校园环境组织学生编织 $ A $,$ B $ 两种中国结。已知编织 $ 1 $ 个 $ A $ 种中国结和 $ 2 $ 个 $ B $ 种中国结需用绳 $ 180 $ $ cm $;编织 $ 2 $ 个 $ A $ 种中国结和 $ 3 $ 个 $ B $ 种中国结需用绳 $ 310 $ $ cm $。
(1) 求编织 $ 1 $ 个 $ A $ 种、$ 1 $ 个 $ B $ 种中国结分别需要绳子的长度。(4 分)
(2) 为满足校园环境的布置需求,需要编织两种中国结共 $ 100 $ 个,其中 $ A $ 种中国结的数量不少于 $ B $ 种中国结数量的一半。当编织 $ A $ 种中国结多少个时所需的总用绳量最少? 最少用绳量是多少? (6 分)

答案： 22.解：
(1)设编织1个A种、1个B种中国结分别需要绳子的长度为$x$cm，$y$cm。由题意，得$\begin{cases}x + 2y = 180\\2x + 3y = 310\end{cases}$解得$\begin{cases}x = 80\\y = 50\end{cases}$故编织1个A种、1个B种中国结分别需要绳子长度为80cm，50cm。
(2)设编织A种中国结$a$个，总用绳量为$s$cm，则由题意，得$a \geq \frac{1}{2}(100 - a)$，解得$a \geq \frac{100}{3}$，又$s = 80a + 50(100 - a)=5000 + 30a$。因为$a$为整数，所以$a \geq 34$。所以当$a = 34$时，$s$有最小值，且为$5000 + 30 × 34 = 6020$，故当编织A种中国结34个时所需的总用绳量最少，最少用绳量是6020cm。