《2025年期末直通车八年级数学上册人教版》

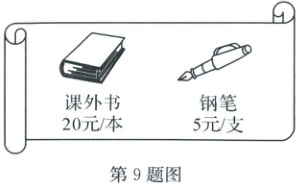
9. （2025·衢州柯城）小柯用150元钱购买课外书和钢笔共10件，课外书和钢笔的单价如下图所示，则小柯最多能买几本课外书？

答案： 9.解:设购买课外书x本，钢笔(10−x)支。由题意，得$20x + 5(10−x) \leq 150$，解得$x \leq \frac{20}{3}$。因为x是正整数，所以x的最大值为6。
答:小柯最多能买6本课外书。

1. (2024·宁波鄞州)$y$减2的差不大于0，用不等式表示为(D)

A.$y - 2 ＞ 0$
B.$y - 2 ＜ 0$
C.$y - 2 ≥ 0$
D.$y - 2 ≤ 0$

答案： 1.D

2. (2024·诸暨)下列判断不正确的是(D)

A.若$a ＞ b$，则$a + 2 ＞ b + 2$
B.若$a ＞ b$，则$-2a ＜ -2b$
C.若$2a ＞ 2b$，则$a ＞ b$
D.若$a ＞ b$，则$ac^2 ＞ bc^2$

答案： 2.D

3. (2024·丽水莲都)若$x = 3$是某个一元一次不等式的一个解，则这个一元一次不等式可能是(D)

A.$2x - 1 ≤ 3$
B.$-3x + 1 ≥ 4$
C.$6x + 2 ＞ 11x - 3$
D.$-\frac{1}{2}x + 4 ＜ 1 + \frac{5}{2}x$

答案： 3.D

4. (2024·浦江)若关于$x$的不等式组$\begin{cases}x ＞ -a,\\x ≥ -b\end{cases}$的解集为$x ≥ -b$，则下列各式正确的是(A)

A.$a ＞ b$
B.$a ＜ b$
C.$a ≤ b$
D.$b ≤ a$

答案： 4.A

5. (2024·杭州西湖)甲、乙两人去超市购物，超市正在举办摸彩活动，单次消费金额每满100元可以拿到1张摸彩券。已知甲一次购买5盒饼干拿到3张摸彩券，乙一次购买5盒饼干与1个蛋糕拿到4张摸彩券。若每盒饼干的售价为$x$元，每个蛋糕的售价为120元，则$x$的取值范围是(C)

A.$56 ≤ x ＜ 76$
B.$56 ≤ x ＜ 80$
C.$60 ≤ x ＜ 76$
D.$60 ≤ x ＜ 80$

答案： 5.C

6. (2024·舟山定海)定义运算：对于实数$a$，$b$，$c$，$mid\{a,b,c\} = b(a ≥ b ≥ c)$。例如，$mid\{1,2,3\} = 2$，$mid\{-1,2,-3\} = -1$，$mid\{1,2,2\} = 2$。若$mid\{-x - 3,x + 2,\frac{1}{2}x - 1\} = k$，对于某个确定的$k$，有且只有一个$x$使等式成立，则$k$的取值范围是(A)

A.$k ＞ -\frac{1}{2}$或$k ＜ -\frac{5}{3}$
B.$-6 ≤ k ≤ -\frac{5}{2}$
C.$-\frac{5}{3} ≤ k ≤ -\frac{1}{2}$
D.$k ＞ -\frac{1}{2}$或$k ＜ -4$

答案： 6.A解析:①$−x−3 \geq x + 2 \geq \frac{1}{2}x−1$，$−6 \leq x \leq −\frac{5}{2}$。此时，$k = x + 2$，$−4 \leq k \leq −\frac{1}{2}$；②$−x−3 \geq \frac{1}{2}x−1 \geq x + 2$，$x \leq −6$，$k = \frac{1}{2}x−1$，$k \leq −4$；③$x + 2 \geq −x−3 \geq \frac{1}{2}x−1$，$−\frac{5}{2} \leq x \leq −\frac{4}{3}$，$k = −x−3$，$−\frac{5}{3} \leq k \leq −\frac{1}{2}$；④$x + 2 \geq \frac{1}{2}x−1 \geq −x−3$，$x \geq −\frac{4}{3}$，$k = \frac{1}{2}x−1$，$k \geq −\frac{5}{3}$；⑤$\frac{1}{2}x−1 \geq −x−3 \geq x + 2$，无解；⑥$\frac{1}{2}x−1 \geq x + 2 \geq −x−3$，$x \geq −\frac{5}{2}$且$x \leq −6$，无解。因为对于某个确定的k,有且只有一个x使等式成立，所以以上k的取值范围取不重叠的部分，即$k ＞ −\frac{1}{2}$或$k ＜ −\frac{5}{3}$，故选A。(或画出数轴，由数轴易知k的取值范围)