《2025年期末直通车八年级数学上册人教版》

1. (2025·嵊州)根据下列图形提供的角度,不能用一条直线把一个三角形分成两个等腰三角形的是 (D)

答案： 1.D

2. (2024·金华金东、兰溪、浦江)如图,在等腰直角三角形纸板△ABC中,AB=AC=10。现要从中剪出一个尽可能大的正方形,则能剪出的最大正方形的面积是 (C)

A.$\dfrac{100}{9}$
B.$\dfrac{200}{9}$
C.25
D.50

答案：
2.C解析:如图，过点A作BC的垂线交BC于点D，过点D分别作DM⊥AB，DN⊥AC。所以AM=MD=DN=AN=$\frac{1}{2}$AB=5，∠BAC=∠AMD=∠MDN=∠DNA=90°。所以正方形AMDN即为最大正方形，S正方形AMDN=5×5=25。故选C。

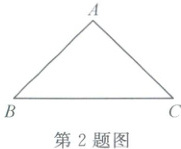
3. (2024·丽水莲都)如图,在等腰三角形ABC中,AB=AC=4,E为BC的中点,连结AE。以BC为边向左作△BCD,且∠BCD=90°,BD//AC。连结DE,记△CDE和△ABE的面积分别为$S_1$和$S_2$,则$\dfrac{3}{2}S_1 - S_2$的最大值是 (D)

A.4
B.6
C.$4\sqrt{2}$
D.8

答案：
3.D解析:如图，延长AE，交BD于点H，并连结CH，则易证HE=AE，△DCH≌△AHC。因为AE=$\frac{1}{2}$AH=$\frac{1}{2}$DC，所以$\frac{3}{2}$S₁ - S₂=$\frac{3}{2}$×$\frac{1}{2}$×DC·CE - $\frac{1}{2}$·BE·AE=$\frac{3}{2}$·AE·CE - $\frac{1}{2}$·CE·AE=AE·CE=$\frac{1}{2}$·2AE·CE≤$\frac{1}{2}$(AE² + CE²)=$\frac{1}{2}$×16=8。故选D。

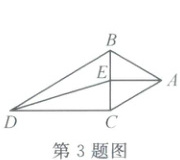
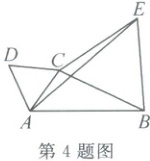
4. (2025·宁波海曙)如图,在△ABC中,AC=2,AB=4,分别以AC,BC为边向外作等边△ACD和等边△BCE,连结AE。在△ABC的边BC变化过程中,当AE取最长时,则BC的长为 (A)

A.$2\sqrt{7}$
B.$\sqrt{29}$
C.$\sqrt{19}$
D.$2\sqrt{5}$

答案：
4.A解析:如图1，连结BD，易证△DCB≌△ACE，所以AE=DB。又因为DB≤AD + AB=6，所以当AD，AB共线，且点A在D，B之间时，BD取得最大值。此时，如图2，过点C作CH⊥BD，H为垂足，则易得BC²=CH² + BH²=3 + 25=28，即BC=2√7。故选A。