第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
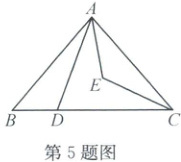
5. (2025·宁波鄞州)如图,在△ABC中,AB=AC,∠BAC=80°,D是边BC上一点(不与B,C重合),∠DAC和∠BCA的平分线交于点E。
(1)若∠BAD=20°,则∠AEC的度数为
(2)记∠DAE和∠ACE的度数之和为m,则m的取值范围为
(1)若∠BAD=20°,则∠AEC的度数为
125°
。(2)记∠DAE和∠ACE的度数之和为m,则m的取值范围为
25° < m < 65°
。
答案:
5.
(1)125°
(2)25° < m < 65° 解析:
(1)∠AEC=90° + $\frac{1}{2}$∠ADC=90° + $\frac{1}{2}$(∠B + ∠BAD)=90° + $\frac{1}{2}$×(50° + 20°)=125°。
(2)m=∠DAE + ∠ACE=$\frac{1}{2}$(180° - ∠ADC)=90° - $\frac{1}{2}$∠ADC=90° - $\frac{1}{2}$(∠B + ∠BAD)=90° - $\frac{1}{2}$(50° + ∠BAD)=65° - $\frac{1}{2}$∠BAD。又因为0° < ∠BAD < 80°,所以25° < m < 65°。
(1)125°
(2)25° < m < 65° 解析:
(1)∠AEC=90° + $\frac{1}{2}$∠ADC=90° + $\frac{1}{2}$(∠B + ∠BAD)=90° + $\frac{1}{2}$×(50° + 20°)=125°。
(2)m=∠DAE + ∠ACE=$\frac{1}{2}$(180° - ∠ADC)=90° - $\frac{1}{2}$∠ADC=90° - $\frac{1}{2}$(∠B + ∠BAD)=90° - $\frac{1}{2}$(50° + ∠BAD)=65° - $\frac{1}{2}$∠BAD。又因为0° < ∠BAD < 80°,所以25° < m < 65°。
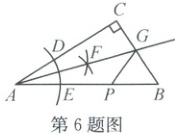
6. (2024·长兴)如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,以点A为圆心,适当长为半径作弧,与边AB,AC分别相交于点E,D,再分别以这两个交点为圆心,以大于$\dfrac{1}{2}DE$的长为半径作弧,两弧交于点F,作射线AF交边BC于点G。P为AB上一动点,则GP的最小值是
$\frac{4}{3}$
。
答案:
6.$\frac{4}{3}$解析:如图,过点G作GH⊥AB于点H,有∠ACG=∠AHG=90°,AG=AG,所以Rt△ACG≌Rt△AHG(HL),可知点G为固定点,当GP垂直于AB时,点P与点H重合时,取GP最小值。因为Rt△AGC≌Rt△AGH,所以AH=AC,CG=GH。因为AB=5,BC=3,所以AH=AC =4,HB=1,BG=3 - CG。所以1² + CG²=(3 - CG)²,GPmin =CG=GH=$\frac{4}{3}$。

6.$\frac{4}{3}$解析:如图,过点G作GH⊥AB于点H,有∠ACG=∠AHG=90°,AG=AG,所以Rt△ACG≌Rt△AHG(HL),可知点G为固定点,当GP垂直于AB时,点P与点H重合时,取GP最小值。因为Rt△AGC≌Rt△AGH,所以AH=AC,CG=GH。因为AB=5,BC=3,所以AH=AC =4,HB=1,BG=3 - CG。所以1² + CG²=(3 - CG)²,GPmin =CG=GH=$\frac{4}{3}$。

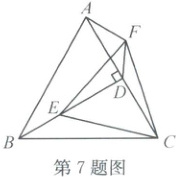
7. (2024·湖州南浔)如图,已知△ABC是边长为2的等边三角形,E为高BD上的动点。连结CE,将线段CE绕点C顺时针旋转60°得到CF。连结AF,EF,DF,则DF的最小值是
$\frac{1}{2}$
。
答案:
7.$\frac{1}{2}$解析:在△BCE和△ACF中,BC=AC,∠BCA=∠ECF=60°,∠ECA=∠ECA。所以∠BCE=∠ACF。因为EC=FC,所以△BCE≌△ACF(SAS),可知点F在射线AF上运动。如图,当DF'⊥AF'时,DF'取最小值。因为等边三角形ABC,BD垂直平分AC,所以BD平分∠ABC,所以∠CBD=30°,所以∠CAF'=30°,所以∠ADF'=60°。所以DF'=$\frac{1}{2}$AD=$\frac{1}{2}$,即DF的最小值为$\frac{1}{2}$。

7.$\frac{1}{2}$解析:在△BCE和△ACF中,BC=AC,∠BCA=∠ECF=60°,∠ECA=∠ECA。所以∠BCE=∠ACF。因为EC=FC,所以△BCE≌△ACF(SAS),可知点F在射线AF上运动。如图,当DF'⊥AF'时,DF'取最小值。因为等边三角形ABC,BD垂直平分AC,所以BD平分∠ABC,所以∠CBD=30°,所以∠CAF'=30°,所以∠ADF'=60°。所以DF'=$\frac{1}{2}$AD=$\frac{1}{2}$,即DF的最小值为$\frac{1}{2}$。

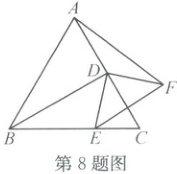
8. (2025·兰溪)如图,在边长为4的等边△ABC中,D是AC的中点,E是直线BC上一动点,连结BD,DE,将线段DE绕点D逆时针旋转90°,得到线段DF,连结EF,AF。
(1)当点E是线段BC的中点时,EF的长为
(2)在点E的运动过程中,线段AF长度最小时,点D到AF的距离为
(1)当点E是线段BC的中点时,EF的长为
2√2
。(2)在点E的运动过程中,线段AF长度最小时,点D到AF的距离为
√3
。
答案:
8.
(1)2√2
(2)√3解析:
(1)EF=$\sqrt{2}$DE=BC=2√2。
(2)如图,延长BD至点A',使DA'=DA,并连结EA',再过点A'作A'E₀⊥BC延长线,E₀'为垂足,再过点D作DH⊥A'E₀,H为垂足,易证△A'DE≌△ADF,则A'E=AF。由A'为定点,易知当E在E₀'处时,A'E取得最小值A'E₀,此时DH=$\frac{\sqrt{3}}{2}$A'D=$\frac{\sqrt{3}}{2}$AD=$\frac{\sqrt{3}}{4}$AC=√3。

8.
(1)2√2
(2)√3解析:
(1)EF=$\sqrt{2}$DE=BC=2√2。
(2)如图,延长BD至点A',使DA'=DA,并连结EA',再过点A'作A'E₀⊥BC延长线,E₀'为垂足,再过点D作DH⊥A'E₀,H为垂足,易证△A'DE≌△ADF,则A'E=AF。由A'为定点,易知当E在E₀'处时,A'E取得最小值A'E₀,此时DH=$\frac{\sqrt{3}}{2}$A'D=$\frac{\sqrt{3}}{2}$AD=$\frac{\sqrt{3}}{4}$AC=√3。

9. (2025·龙泉、庆元)在数学活动课上,同学们用边长为m,n的两个正方形A,B(如图1)进行摆放,其中m>n。现有两种摆放方式:方式一,如图2,将正方形B放在正方形A内部;方式二,如图3,将正方形A,B并列放置在边长为(m+n)的正方形内部。若记图1中正方形A,B的面积之和为a,记图2、图3中阴影部分的面积分别为b,c,解答下列问题:
(1)用m,n的代数式表示c。
(2)若△ABC的三边长分别为a,b,c。试猜想△ABC是哪一类三角形,并证明你的猜想。
(3)已知直角三角形的两边长为m,n,且m,n为整数,当a=25时,求直角三角形第三边的长。
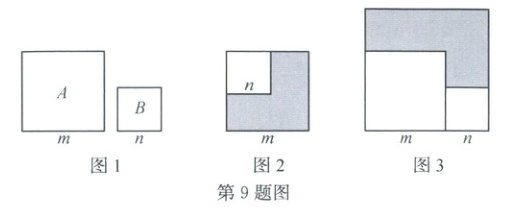
(1)用m,n的代数式表示c。
(2)若△ABC的三边长分别为a,b,c。试猜想△ABC是哪一类三角形,并证明你的猜想。
(3)已知直角三角形的两边长为m,n,且m,n为整数,当a=25时,求直角三角形第三边的长。

答案:
9.解:
(1)c=(m + n)² - m² - n²=2mn。
(2)猜想为直角三角形。证明:因为a=m² + n²,b=m² - n²,c=2mn,所以a²=(m² + n²)²=m⁴ + 2m²n² + n⁴,b² + c²=(m² - n²)² + (2mn)²=m⁴ - 2m²n² + n⁴ + 4m²n²=m⁴ + 2m²n² + n⁴,所以b² + c²=a²,所以△ABC是直角三角形。
(3)据题意得a=m² + n²=25,m²=25 - n²,m²=(5 + n)(5 - n)。据题意,得n为大于0且小于5的整数,且m>n,所以m=4,n=3。①当m,n为直角边长时,第三边长为5;②当m为斜边长时,第三边长为√7。
(1)c=(m + n)² - m² - n²=2mn。
(2)猜想为直角三角形。证明:因为a=m² + n²,b=m² - n²,c=2mn,所以a²=(m² + n²)²=m⁴ + 2m²n² + n⁴,b² + c²=(m² - n²)² + (2mn)²=m⁴ - 2m²n² + n⁴ + 4m²n²=m⁴ + 2m²n² + n⁴,所以b² + c²=a²,所以△ABC是直角三角形。
(3)据题意得a=m² + n²=25,m²=25 - n²,m²=(5 + n)(5 - n)。据题意,得n为大于0且小于5的整数,且m>n,所以m=4,n=3。①当m,n为直角边长时,第三边长为5;②当m为斜边长时,第三边长为√7。
查看更多完整答案,请扫码查看


