《2025年期末直通车八年级数学上册人教版》

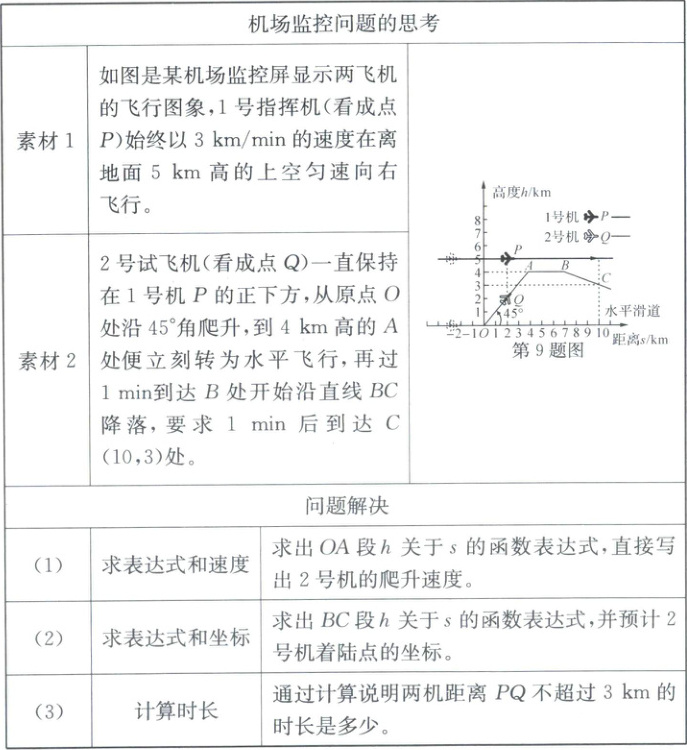
9. (2024·长兴)某校八年级学生在数学课上进行了项目化学习研究,请你尝试帮助他们解决相关问题。

答案： 9.解:
(1)因为$2$号飞机爬升角度为$45^{\circ}$，所以$OA$上的点的横纵坐标相同。所以$A(4,4)$。设$OA$的表达式为$h = ks$，所以$4k = 4$。所以$k = 1$。所以$OA$的表达式为$h = s$。 $2$号机的爬升速度为$3\sqrt{2}km/min$。
(2)设$BC$的表达式为$h = ms + n$，由题意，得点$B$的横坐标为$4 + 3×1 = 7$，所以$B(7,4)$。又$C(10,3)$，所以$\begin{cases}7m + n = 4\\10m + n = 3\end{cases}$，解得$\begin{cases}m=-\frac{1}{3}\\n=\frac{19}{3}\end{cases}$，所以$BC$的表达式为$h=-\frac{1}{3}s+\frac{19}{3}$。令$h = 0$，则$s = 19$。所以预计$2$号机着陆点的坐标为$(19,0)$。
(3)因为$PQ$不超过$3km$，所以$5 - h\leqslant\begin{cases}3(0\leqslant s\leqslant4)\\5 - s(4\leqslant s\leqslant7)\\5 - (-\frac{1}{3}s+\frac{19}{3})\leqslant3(7\leqslant s\leqslant19)\end{cases}$，解得$2\leqslant s\leqslant13$。所以两机距离$PQ$不超过$3km$的时长为$(13 - 2)÷3=\frac{11}{3}(min)$。