《2025年期末直通车八年级数学上册人教版》

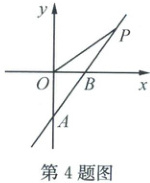
4. (2024·杭州余杭)如图,一次函数 $ y = kx - 8 $ 的图象交 $ y $ 轴于点 $ A $,交 $ x $ 轴于点 $ B $,且 $ \frac { O B } { O A } = \frac { 3 } { 4 } $,$ P $ 是第一象限内直线 $ AB $ 上的动点,连结 $ OP $。
(1)点 $ B $ 的坐标为(6,0), $ k = $$\frac{4}{3}$。
(2)设点 $ P ( x, y ) $,则 $ \triangle OBP $ 的面积 $ S $ 与 $ x $ 的函数表达式为S = 4x - 24(x＞6)。

答案： 4.
(1)(6,0) $\frac{4}{3}$
(2)S = 4x - 24(x＞6)

5. (2024·丽水莲都)已知直线 $ l _ { 1 } : y = k x + 2 + k ( k \neq 0 ) $ 和直线 $ l _ { 2 } : y = x + 3 $。若直线 $ l _ { 1 }, l _ { 2 } $ 与 $ y $ 轴所围成的三角形面积记作 $ S $。
(1)当 $ k = - 1 $ 时,$ S $ 的值是1。
(2)当 $ 2 \leqslant S \leqslant 3 $ 时,$ k $ 的取值范围是5 ≤ k ≤ 7或 - 5 ≤ k ≤ - 3。

答案： 5.
(1)1
(2)5 ≤ k ≤ 7或 - 5 ≤ k ≤ - 3 解析:
(1)y = kx + 2 + k(k ≠ 0)，得y = k(x + 1) + 2，所以l₁过定点P(-1,2)，且点P也在l₂上，画出图象(图略)，易知S = $\frac{1}{2}$|2 + k - 3| = $\frac{1}{2}$|k - 1|，所以当k = - 1时，S = 1。
(2)当2 ≤ S ≤ 3时，则4 ≤ |k - 1| ≤ 6，解得5 ≤ k ≤ 7或 - 5 ≤ k ≤ - 3。

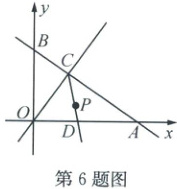
6. (2025·义乌)如图,在平面直角坐标系 $ x O y $ 中,直线 $ y = - \frac { 3 } { 4 } x + 6 $ 交 $ x $ 轴于点 $ A $,交 $ y $ 轴于点 $ B $,过坐标原点 $ O $ 作直线 $ AB $ 的垂线交 $ AB $ 于点 $ C $,$ \angle O C A $ 的平分线 $ C D $ 交 $ x $ 轴于点 $ D $。
(1)线段 $ O C $ 的长为$\frac{24}{5}$。
(2)若一动点 $ P $ 在射线 $ C D $ 上运动,连结 $ A P $,当 $ \triangle A C P $ 为直角三角形时,点 $ P $ 的坐标为$\frac{104}{25}$, - $\frac{128}{25}$)或($\frac{88}{25}$, - $\frac{16}{25}$。

答案：
6.
(1)$\frac{24}{5}$
(2)($\frac{104}{25}$, - $\frac{128}{25}$)或($\frac{88}{25}$, - $\frac{16}{25}$) 解析:
(1)因为直线y = - $\frac{3}{4}$x + 6交x轴于点A，交y轴于点B，所以B(0,6)，A(8,0)，所以AB = $\sqrt{6² + 8²}$ = 10。由等面积可知，AB·OC = OA·OB，所以OC = $\frac{OA·OB}{AB}$ = $\frac{8×6}{10}$ = $\frac{24}{5}$。

(2)如图1，分别过点D作DE⊥CO，DF⊥CA，垂足分别为点E，F。在Rt△OBC中，BC = $\sqrt{OB² - OC²}$ = $\frac{18}{5}$，所以AC = AB - BC = $\frac{32}{5}$。过点C作CK⊥OB于点K，根据等面积可得CK = $\frac{OC·BC}{OB}$ = $\frac{72}{25}$。在直角三角形OKC中，OK = $\sqrt{OC² - CK²}$ = $\frac{96}{25}$。所以C($\frac{72}{25}$,$\frac{96}{25}$)，又由CD平分∠OCA得DE = DF，所以$\frac{OD}{DA}$ = $\frac{S_{△OCD}}{S_{△CDA}}$ = $\frac{OC}{CA}$ = $\frac{3}{4}$，所以OD = $\frac{3}{7}$OA = $\frac{24}{7}$，即点D为($\frac{24}{7}$,0)，所以易得直线CD的解析式为y = - 7x + 24。因为∠OCA = 90°，CD平分∠OCA，所以∠ACP = 45°。
①如图2，当∠CAP = 90°时，则AC = AP，过点A作EF//y轴，过点C作CE⊥EF于点E，PF⊥EF于点F，则∠E = ∠F = 90°，所以CE = 8 - $\frac{72}{25}$ = $\frac{128}{25}$，AE = $\frac{96}{25}$。

因为∠CAP = 90°，所以∠CAE = 90° - ∠PAF = ∠APF。在△ACE和△PAF中，$\begin{cases}∠E = ∠F\\∠CAE = ∠APF\\AC = AP\end{cases}$，所以△ACE≌△PAF(AAS)，所以AF = CE = $\frac{128}{25}$，PF = AE = $\frac{96}{25}$，所以x_P = 8 - $\frac{96}{25}$ = $\frac{104}{25}$，y_P = - $\frac{128}{25}$，所以P($\frac{104}{25}$, - $\frac{128}{25}$)；
②如图3，当∠CPA = 90°时，则AP = CP，过点P作MN//x轴，过点C作CM⊥MN于点M，过点A作AN⊥MN于点N，同理可得△CPM≌△PAN(AAS)，所以设MP = AN = a，CM = PN = b，则$\begin{cases}b - a = \frac{96}{25}\\a + b = \frac{128}{25}\end{cases}$，解得$\begin{cases}a = \frac{16}{25}\\b = \frac{112}{25}\end{cases}$，所以x_P = 8 - $\frac{112}{25}$ = $\frac{88}{25}$，y_P = - $\frac{16}{25}$，所以P($\frac{88}{25}$, - $\frac{16}{25}$)。

综上，点P的坐标为($\frac{104}{25}$, - $\frac{128}{25}$)或($\frac{88}{25}$, - $\frac{16}{25}$)。

7. (2025·松阳)如图,已知一次函数 $ y = k x + b ( k \neq 0 ) $ 图象分别与 $ x $ 轴、$ y $ 轴交于点 $ A ( 2 \sqrt { 3 }, 0 ) $,$ B ( 0, 2 ) $,点 $ P $ 在 $ x $ 轴上运动,连结 $ P B $。
(1)当点 $ P $ 运动到 $ O A $ 中点时,求 $ \triangle P A B $ 的面积。
(2)将 $ \triangle O B P $ 沿 $ B P $ 折叠,点 $ O $ 的对应点记为 $ O ^ { \prime } $。若点 $ O ^ { \prime } $ 恰好落在直线 $ A B $ 上,求此时 $ \angle A P B $ 的度数。
(3)将直线 $ B P $ 绕点 $ P $ 顺时针旋转 $ 30 ^ { \circ } $,交直线 $ A B $ 于点 $ Q $。在点 $ P $ 的运动过程中,是否存在某一位置,使得 $ \triangle P B Q $ 为等腰三角形?若存在,请直接写出点 $ P $ 的坐标;若不存在,请说明理由。

答案： 7.解:
(1)$S_{△PAB}$ = $\frac{1}{2}S_{△OBA} $= $\frac{1}{2}$×$\frac{1}{2}$×2$\sqrt{3}$×2 = $\sqrt{3}$。
(2)由已知易得BO' = BO = 2。①若点O'在AB的延长线上，则易知点P在x轴负半轴上，则∠PBO = $\frac{1}{2}$(180° - ∠OBA) = 60°，所以∠APB = 30°。②若点O'在线段AB上，则易知点P在线段OA上，所以∠PBA = $\frac{1}{2}$∠OBA = 30°，∠APB = 180° - ∠A - ∠PBA = 120°。
(3)点P的坐标为(-2$\sqrt{3}$,0)或(-4 + 2$\sqrt{3}$,0)或($\frac{2}{3}\sqrt{3}$,0)或(4 + 2$\sqrt{3}$,0)。