《2025年期末直通车八年级数学上册人教版》

1. (2024·绍兴柯桥)等腰三角形的顶角与其一个底角的度数的比值$k$称为这个等腰三角形的“特征值”。若在等腰三角形$ABC$中，$\angle A = 80^{\circ}$，则它的特征值$k =$(C)

A.$\frac{8}{5}$
B.$\frac{1}{4}$
C.$\frac{8}{5}$或$\frac{1}{4}$
D.$\frac{5}{8}$或$4$

答案： 1.C　解析:分两种情况讨论:当∠A为顶角时，底角的度数为50°，此时特征值k=$\frac{80°}{50°}$=$\frac{8}{5}$;当∠A为底角时，顶角的度数为20°，此时特征值k=$\frac{20°}{80°}$=$\frac{1}{4}$。综上，特征值k为$\frac{8}{5}$或$\frac{1}{4}$。故选C。

2. (2024·宁波北仑)定义:若三角形满足其中两边之和等于第三边的三倍，则称该三角形为“三倍三角形”。若等腰三角形$ABC$是“三倍三角形”，且其中一边长为$3$，则$\triangle ABC$的周长为(C)

A.$8$
B.$12$
C.$8$或$12$
D.$8$或$12$或$16$

答案： 2.C　解析:若△ABC中腰长为3,则可设底边长为a，则三边分别为3,3,a。由题意，得3a=3+3或3+a=3×3,分别解得a=2或a=6(舍去),此时周长为3+3+2=8;若△ABC中底边长为3,设腰长为b,则同理，得2b=9或3+b=3b,分别解得b=4.5或b=1.5(舍去),此时周长为12。故选C。

3. (2025·杭州滨江)在$Rt\triangle ABC$中，$AB = AC$，直线$l$交$BC$于点$E$，交$AC$于点$F$，点$C$关于直线$l$的对称点$D$在边$AB$上，若$CE = 3$，$BE = \sqrt{14}$，则$BD$的长为()

A.$\sqrt{7}\pm\sqrt{2}$
B.$\sqrt{7}$
C.$\sqrt{14}\pm\sqrt{2}$
D.$\sqrt{14}$

答案：
3.A　解析:过点E作EH⊥AB,H为垂足，并连结DE,AE,则BH=$\sqrt{7}$。又由点D、点C关于l对称，得DE=CE=3。所以DH=$\sqrt{DE^{2}-HE^{2}}$=$\sqrt{2}$。①若点D在线段BH上,则BD=BH−DH=$\sqrt{7}$−$\sqrt{2}$;②若点D在BH延长线上,则BD=BH+DH=$\sqrt{7}$+$\sqrt{2}$。又由∠CEF=$\frac{1}{2}$∠DEC≤90°＜∠AEC,得点F恒在线段AC上。故BD=$\sqrt{7}$±$\sqrt{2}$。故选A。

4. (2025·宁波鄞州)已知$\triangle ABC$的周长为$16$，$AB = 6$，当$AC$的值为6或5或4时，$\triangle ABC$是等腰三角形。

答案： 4.6或5或4

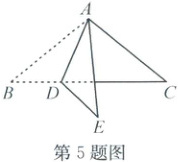
5. (2024·嘉兴)如图，在$\triangle ABC$中，$AB = AC$，$\angle B = 40^{\circ}$，$D$是$BC$上一动点，将$\triangle ABD$沿$AD$折叠得到$\triangle ADE$，当$\triangle ADE$与$\triangle ABC$重叠部分是直角三角形时，$\angle BAD$的度数为25°或50°或75°。

答案： 5.25°或50°或75°　解析:①当点E在BC下方或BC上时，若重叠部分为直角三角形，则当AD⊥BC时，∠BAD=90°−∠B=50°;当AE⊥BC时,所以∠BAD=$\frac{1}{2}$(90°−∠B)=25°;②当点E在BC上方时，若重叠部分为直角三角形，则∠CAE=90°−∠E=50°,所以∠BAD=$\frac{1}{2}$(∠BAC+∠CAE)=75°。综上,∠BAD=25°或50°或75°。

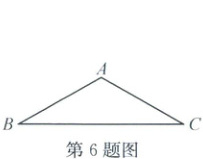
6. (2024·诸暨)如图，在$\triangle ABC$中，$\angle ABC = 30^{\circ}$，$AB = AC = 2\sqrt{3}$，$D$是边$BC$上的点，将$\triangle ACD$沿$AD$折叠得到$\triangle AED$，$E$是点$C$的对称点。若$\angle CDE = 120^{\circ}$，则$CD$的长是4或2。

答案：
6.4或2　解析:①当∠ADC≤90°时,如图1,因为∠CDE=120°且折叠，所以∠ADC=60°。由题可知,AB=AC且∠B=30°,∠C=30°,所以∠CAD=90°。取CD的中点P,易得AD=DP=$\frac{1}{2}$CD。因为AC=2$\sqrt{3}$,所以AD=2,CD=4;　②当∠ADC＞90°时，如图2,连结CE,可知AD垂直平分CE，垂足为点N,易得CN=$\sqrt{3}$。因为∠CDE=120°,所以∠DEC=180°−120°−30°=30°,∠NDE=60°,易得ND=$\frac{1}{2}$ED=$\frac{1}{2}$CD。在△CND中,CN²+ND²=CD²,所以ND=1,CD=2。综上,CD的长是4或2。