第110页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
7. 如图,每个图形都是由若干个棋子围成的正方形图案,图案每条边(包括两个端点)上都有 $n(n \geq 2)$ 个棋子,设每个图案棋子的总数为 $S$。当 $S = 2024$ 时,$n$ 的值为(

A.$504$
B.$505$
C.$506$
D.$507$
D
)
A.$504$
B.$505$
C.$506$
D.$507$
答案:
7.D
8. 如图,在 $Rt\triangle ABC$ 中,$\angle A = 90^{\circ}$,将 $\triangle ABC$ 沿 $DE$ 翻折,使得点 $C$ 与点 $B$ 重合。若 $AB = 6$,$AC = 8$,则折痕 $DE$ 的长为(
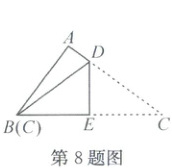
A.$4$
B.$\frac{15}{4}$
C.$5$
D.$\frac{25}{4}$
B
)
A.$4$
B.$\frac{15}{4}$
C.$5$
D.$\frac{25}{4}$
答案:
8.B
9. 甲、乙两人沿同一跑道从 $A$ 处跑到 $B$ 处。乙比甲先出发 $2$ 分钟,甲的速度为每分钟 $150$ 米。若两人之间的路程 $y$(米)与甲出发的时间 $x$(分钟)的关系如图所示,则 $A$,$B$ 两地的路程为(
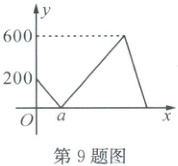
A.$1800$ 米
B.$2000$ 米
C.$2400$ 米
D.$2500$ 米
C
)
A.$1800$ 米
B.$2000$ 米
C.$2400$ 米
D.$2500$ 米
答案:
9.C
10. 如图,$D$,$E$ 为等边 $\triangle ABC$ 边 $AB$,$BC$ 上的点,连结 $DE$,$\angle ADE$ 和 $\angle DEC$ 的平分线恰好过 $AC$ 边上同一点 $F$。若要知道 $\triangle ABC$ 的周长,只需要知道下列哪个三角形的周长? 该三角形是(
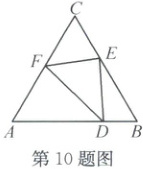
A.$\triangle ADF$
B.$\triangle BDE$
C.$\triangle CEF$
D.$\triangle DEF$
B
)
A.$\triangle ADF$
B.$\triangle BDE$
C.$\triangle CEF$
D.$\triangle DEF$
答案:
10.B 解析:①如图,过点F作FP//CB,点P在AB上,若点D在线段PB上,则∠FDP=∠FDE<∠FPA=∠C=60°,
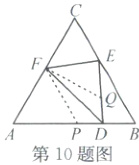
故可在线段DE上作∠FQE=60°,可易证△CEF≌△QEF,所以CE=QE,FQ=CF,也可易证△FQD≌△FPD,所以FQ=FP,QD=PD,所以CF=FA,DE=CE+PD,所以C_{DEB}=DE+EB+DB=CB+DB+PD=$\frac{1}{2}$C_{△CAB};②若点D在线段AP上,同理可证。故选B。
10.B 解析:①如图,过点F作FP//CB,点P在AB上,若点D在线段PB上,则∠FDP=∠FDE<∠FPA=∠C=60°,

故可在线段DE上作∠FQE=60°,可易证△CEF≌△QEF,所以CE=QE,FQ=CF,也可易证△FQD≌△FPD,所以FQ=FP,QD=PD,所以CF=FA,DE=CE+PD,所以C_{DEB}=DE+EB+DB=CB+DB+PD=$\frac{1}{2}$C_{△CAB};②若点D在线段AP上,同理可证。故选B。
11. 在平面直角坐标系中,将点 $A(0,1)$ 向下平移 $1$ 个单位长度,得到的点的坐标为
(0,0)
。
答案:
11.(0,0)
12. 在直角三角形中,两条直角边的长为 $2$ 和 $3$,则斜边长为________。
答案:
12.√13
13. $[a]$ 表示不超过 $a$ 的最大整数,则 $[1.6]$ 的值为
1
。
答案:
13.1
14. 一次函数 $y = kx + k^2$ ($k$ 为常数,$k \neq 0$)的图象经过点 $(0,9)$,但不经过第三象限,则 $k$ 的值为
-3
。
答案:
14.-3
15. 已知 $\triangle ABC \cong \triangle ABD$,$\angle BAC = \angle BAD = 30^{\circ}$,$AB = 2$,$BC = BD = \sqrt{2}$,则 $CD$ 的长为
√3±1
。
答案:
15.√3±1
16. 对于一次函数 $y = kx - k - 1$ ($k$ 为常数,$k \neq 0$),当 $1 \leq x \leq 2$ 时,$y$ 有 $3$ 个整数值,则符合条件的整数 $k$ 的值为
2或-2
。
答案:
16.2或-2 解析:①若k>0,则当1≤x≤2时,-1≤y≤k-1,此时若y有3个整数值,则y=-1,0,1,即有1≤k-1<2,解得2≤k<3;②若k<0,则当1≤x≤2时,k-1≤y≤-1。此时若y有3个整数值,则y=-1,-2,-3,即有-4<k-1≤-3,解得-3<k≤-2。综上,k=2或-2。
查看更多完整答案,请扫码查看


