《2025年课课练江苏七年级数学上册苏科版》

例1 如图1.3.1所示,有大小完全相同的两张直角三角形纸片,若将它们的某条边重合,能拼成几种不同形状的四边形?请你画出拼成的四边形,并指出哪个四边形的周长最大.

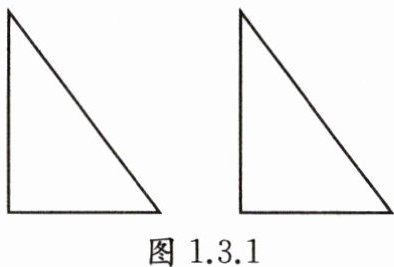
答案：

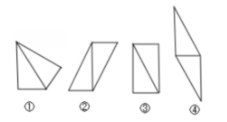
解：能画出4种

第④种周长最大。

(1)“23”应写在射线OE上.
(2)“2025”应写在哪条射线上,为什么?
因为2025÷6=337……3，所以“2025”应写在射线OC上。
(3)请任意写出一条射线上数字的排列规律,并将你的观点与他人交流.
射线OA上数字的排列规律是6n-5（n为正整数）。

答案： 【解析】：
(1)观察图形可知，每6个数为一组，循环依次排列在射线$OA,OB,OC,OD,OE,OF$上。
用$23$除以$6$，$23÷6 = 3\cdots\cdots5$，其中商$3$表示完整的组数，余数$5$表示在新的一组中的位置。
按照从射线$OA$开始按逆时针方向依次排列的规则，余数$5$对应的射线是$OE$，所以“$23$”应写在射线$OE$上。
(2)同样，用$2025$除以$6$，$2025÷6 = 337\cdots\cdots3$。
商$337$表示完整的组数，余数$3$表示在新的一组中的位置。
按照排列规则，余数$3$对应的射线是$OC$，所以“$2025$”应写在射线$OC$上。
(3)以射线$OA$为例，第一组中$OA$上的数字是$1$，第二组中$OA$上的数字是$1 + 6 = 7$，第三组中$OA$上的数字是$7 + 6 = 13$，以此类推。
可以发现射线$OA$上数字的排列规律是$6n - 5$（$n$为正整数），因为当$n = 1$时，$6×1 - 5 = 1$；当$n = 2$时，$6×2 - 5 = 7$ ，符合射线$OA$上数字的排列情况。
【答案】：
(1)$OE$
(2)因为$2025÷6 = 337\cdots\cdots3$，所以“$2025$”应写在射线$OC$上。
(3)射线$OA$上数字的排列规律是$6n - 5$（$n$为正整数）。

例3 如图1.3.3是自动测温仪记录的图象,它反映了A地春季某天气温T随时间t的变化而变化.
(1)从这个图象可知:这一天中最低气温约为-3℃,最高气温约为8℃.
(2)从4时到14时气温随时间变化呈上升状态,请你指出气温随时间变化呈下降状态的时间段.0时到4时和14时到24时

答案： 【解析】：
题目考查了函数图象的信息获取能力。
要求能通过观察图象的纵坐标获取最低和最高气温信息，以及通过图象的升降变化判断气温随时间的变化趋势。
(1)观察图象，找到纵坐标的最小值和最大值，即为最低气温和最高气温。
(2)观察图象在特定时间段内的升降情况，判断气温是上升还是下降。
【答案】：
解：
(1)从图象可知，这一天中最低气温约为$-3℃$，最高气温约为$8℃$。
故答案为：$-3$；$8$。
(2)从图象可以看出，气温随时间变化呈下降状态的时间段有两个：
一是从0时到4时，气温从接近$0℃$下降到$-3℃$；
二是从14时到24时，气温从最高$8℃$下降到较低的温度。
所以，气温随时间变化呈下降状态的时间段是$0$时到$4$时和$14$时到$24$时。