《2025年课课练江苏七年级数学上册苏科版》

8. (1)根据已学知识,我们已经能比较有理数的大小.例如,你会比较$\frac{2023}{2024}与\frac{2024}{2025}$的大小吗？
解：$\frac{2023}{2024} - \frac{2024}{2025} = \frac{2023 × 2025 - 2024^2}{2024 × 2025}$
$= \frac{(2024 - 1)(2024 + 1) - 2024^2}{2024 × 2025}$
$= \frac{2024^2 - 1 - 2024^2}{2024 × 2025}$
$= -\frac{1}{2024 × 2025} ＜ 0$
因此，$\frac{2023}{2024} ＜ \frac{2024}{2025}$。
(2)下面介绍一种新的比较大小的方法：
因为$3-2= 1＞0$,所以$3＞2$；
因为$(-2)-1= -3＜0$,所以$-2＜1$；
因为$(-2)-(-2)= 0$,所以$-2= -2$.
像上面这样,根据两数之差是正数、负数或$0$,判断两数大小关系的方法叫作“作差法”.
“作差法”的一般结论如下：
① 若$a-b＞0$,则$a$＞$b$；② 若$a-b= 0$,则$a$=$b$；③ 若$a-b＜0$,则$a$＜$b$.反之亦然.
(3)试利用“作差法”比较$-\frac{4}{5}与-\frac{5}{6}$的大小.
解：$-\frac{4}{5} - (-\frac{5}{6}) = -\frac{4}{5} + \frac{5}{6}$
$= \frac{-4 × 6 + 5 × 5}{5 × 6}$
$= \frac{-24 + 25}{30}$
$= \frac{1}{30} ＞ 0$
因此，$-\frac{4}{5} ＞ -\frac{5}{6}$。

答案： 【解析】：
本题主要考察有理数的大小比较以及作差法的应用。
(1) 对于$\frac{2023}{2024}$与$\frac{2024}{2025}$，可以通过求它们的差来判断大小。
(2) 这一部分介绍了作差法来比较两个数的大小。具体地，如果$a-b＞0$，则$a＞b$；如果$a-b=0$，则$a=b$；如果$a-b＜0$，则$a＜b$。
(3) 对于$-\frac{4}{5}$与$-\frac{5}{6}$，我们将使用作差法来比较它们的大小。
【答案】：
(1) 解：$\frac{2023}{2024} - \frac{2024}{2025} = \frac{2023 × 2025 - 2024^2}{2024 × 2025}$
$= \frac{(2024 - 1)(2024 + 1) - 2024^2}{2024 × 2025}$
$= \frac{2024^2 - 1 - 2024^2}{2024 × 2025}$
$= -\frac{1}{2024 × 2025} ＜ 0$
因此，$\frac{2023}{2024} ＜ \frac{2024}{2025}$。
(2) ① $＞$ ② $=$ ③ $＜$
(3) 解：$-\frac{4}{5} - (-\frac{5}{6}) = -\frac{4}{5} + \frac{5}{6}$
$= \frac{-4 × 6 + 5 × 5}{5 × 6}$
$= \frac{-24 + 25}{30}$
$= \frac{1}{30} ＞ 0$
因此，$-\frac{4}{5} ＞ -\frac{5}{6}$。

9. 有一种运算游戏,它的规则如下：从若干张“△”和“○”卡片中分别随机抽取$2$张,若抽到“△”卡片,则加上卡片上的数；若抽到“○”卡片,则减去卡片上的数.$4$张卡片上的数经过运算后,结果大的获胜.已知小明和小丽抽到的卡片分别如下：

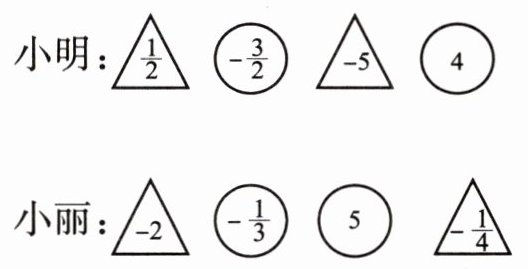
试判断谁会胜出.

答案： 解：小明的运算结果：
$\begin{aligned}&\frac{1}{2}-\left(-\frac{3}{2}\right)+(-5)-4\\=&\frac{1}{2}+\frac{3}{2}-5-4\\=&2 - 9\\=&-7\end{aligned}$
小丽的运算结果：
$\begin{aligned}&-2-\left(-\frac{1}{3}\right)-5+\left(-\frac{1}{4}\right)\\=&-2+\frac{1}{3}-5-\frac{1}{4}\\=&-7+\left(\frac{4}{12}-\frac{3}{12}\right)\\=&-7+\frac{1}{12}\\=&-6\frac{11}{12}\end{aligned}$
因为$-6\frac{11}{12} ＞ -7$，所以小丽胜出。
答：小丽会胜出。