第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
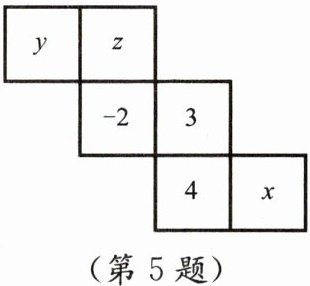
5. 如图,把纸片折叠成正方体后,相对面上的两数都互为相反数,则x+y-z的值为______.

3
答案:
解:由正方体表面展开图可知,“y”与“3”相对,“z”与“4”相对,“-2”与“x”相对。
因为相对面上的两数互为相反数,所以:
y + 3 = 0,解得y = -3;
z + 4 = 0,解得z = -4;
-2 + x = 0,解得x = 2。
则x + y - z = 2 + (-3) - (-4) = 2 - 3 + 4 = 3。
答案:3
因为相对面上的两数互为相反数,所以:
y + 3 = 0,解得y = -3;
z + 4 = 0,解得z = -4;
-2 + x = 0,解得x = 2。
则x + y - z = 2 + (-3) - (-4) = 2 - 3 + 4 = 3。
答案:3
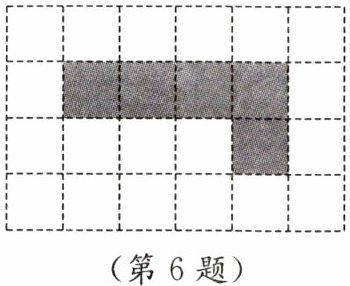
6. 如图,小明利用网格纸做一个正方体盒子,裁剪下涂色部分折叠,发现缺少一个面,请你帮他在图中再拼接一个正方形,使拼接后的图形能折叠成一个封闭的正方体.(将所有符合条件的小方格都涂黑)

答案:


7. 我们知道,数与形之间可以相互转化.在学习“转化 表达”这节课时,小华发现课本上利用图形总结了连续奇数之和的规律,如图所示.
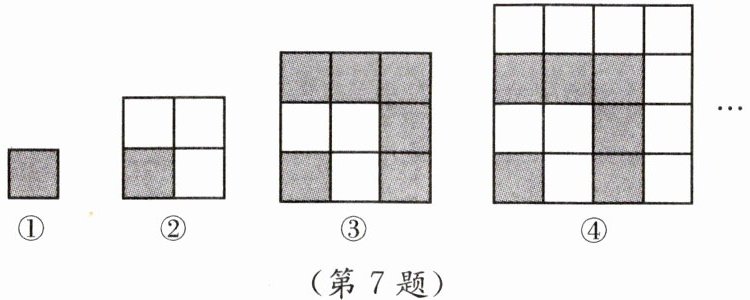
(1) 借助图形,可以得出$1+3+5+7+…+(2n-1)=$______
(2) 小华在课后思考如何借助图形找到连续偶数之和的规律,他做了如下尝试:
]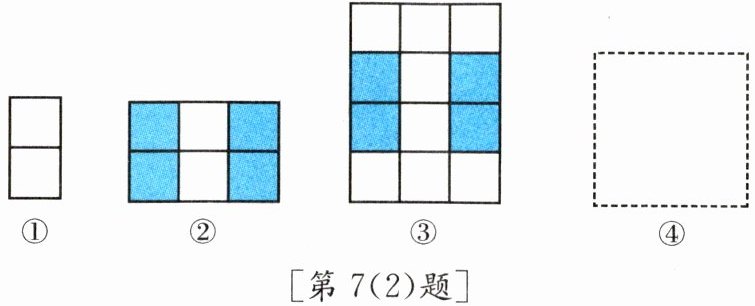
请你画出第④个图,并计算:$2+4+6+8+…+2n=$______

(1) 借助图形,可以得出$1+3+5+7+…+(2n-1)=$______
$n^{2}$
.(2) 小华在课后思考如何借助图形找到连续偶数之和的规律,他做了如下尝试:
]

请你画出第④个图,并计算:$2+4+6+8+…+2n=$______
$n(n + 1)$
.
答案:
【解析】:
(1)要求$1 + 3 + 5 + 7 + \cdots+ (2n - 1)$的结果。
观察图形可知:
第一个图:$1$是一个$1×1$的正方形,$1 = 1^{2}$;
第二个图:$1 + 3 = 4$,$4$是一个$2×2$的正方形,$1 + 3 = 2^{2}$;
第三个图:$1 + 3 + 5 = 9$,$9$是一个$3×3$的正方形,$1 + 3 + 5 = 3^{2}$;
第四个图:$1 + 3 + 5 + 7 = 16$,$16$是一个$4×4$的正方形,$1 + 3 + 5 + 7 = 4^{2}$。
以此类推,$1+3 + 5 + 7+\cdots+(2n - 1)$等于边长为$n$的正方形的面积,即$n^{2}$。
所以$1 + 3 + 5 + 7+\cdots+(2n - 1)=n^{2}$。
(2)先画第④个图:
观察图形规律,第一个图:$2 = 1×2$;
第二个图:$2 + 4 = 6 = 2×3$;
第三个图:$2 + 4 + 6 = 12 = 3×4$。
那么第④个图应该是$2 + 4 + 6 + 8$,图形是一个$4×5$的长方形的一半(从图形排列规律来看),$2 + 4 + 6 + 8 = 4×5 = 20$。
再计算$2 + 4 + 6 + 8+\cdots+ 2n$:
$2=1×2$,$2 + 4 = 2×3$,$2 + 4 + 6 = 3×4$,$\cdots$,$2 + 4 + 6 + 8+\cdots+ 2n=n(n + 1)$。
【答案】:
(1)$n^{2}$;
(2)图略;$n(n + 1)$。
(1)要求$1 + 3 + 5 + 7 + \cdots+ (2n - 1)$的结果。
观察图形可知:
第一个图:$1$是一个$1×1$的正方形,$1 = 1^{2}$;
第二个图:$1 + 3 = 4$,$4$是一个$2×2$的正方形,$1 + 3 = 2^{2}$;
第三个图:$1 + 3 + 5 = 9$,$9$是一个$3×3$的正方形,$1 + 3 + 5 = 3^{2}$;
第四个图:$1 + 3 + 5 + 7 = 16$,$16$是一个$4×4$的正方形,$1 + 3 + 5 + 7 = 4^{2}$。
以此类推,$1+3 + 5 + 7+\cdots+(2n - 1)$等于边长为$n$的正方形的面积,即$n^{2}$。
所以$1 + 3 + 5 + 7+\cdots+(2n - 1)=n^{2}$。
(2)先画第④个图:
观察图形规律,第一个图:$2 = 1×2$;
第二个图:$2 + 4 = 6 = 2×3$;
第三个图:$2 + 4 + 6 = 12 = 3×4$。
那么第④个图应该是$2 + 4 + 6 + 8$,图形是一个$4×5$的长方形的一半(从图形排列规律来看),$2 + 4 + 6 + 8 = 4×5 = 20$。
再计算$2 + 4 + 6 + 8+\cdots+ 2n$:
$2=1×2$,$2 + 4 = 2×3$,$2 + 4 + 6 = 3×4$,$\cdots$,$2 + 4 + 6 + 8+\cdots+ 2n=n(n + 1)$。
【答案】:
(1)$n^{2}$;
(2)图略;$n(n + 1)$。
8. 如图是一张长40 cm,宽30 cm的长方形纸片,要求在长方形纸片的四个角各剪去一个小正方形,使裁剪后的纸片可以折成一个高为10 cm的无盖长方体盒子.
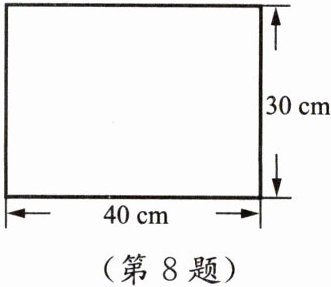
(1) 该如何裁剪呢?请画出示意图(用实线表示剪切线,虚线表示折痕,并标出尺寸).
(2) 求该盒子的容积.

(1) 该如何裁剪呢?请画出示意图(用实线表示剪切线,虚线表示折痕,并标出尺寸).
(2) 求该盒子的容积.
答案:
【解析】:
本题主要考查长方体的展开图及容积计算。
(1)因为要折成一个高为$10cm$的无盖长方体盒子,所以在长方形纸片的四个角各剪去一个边长为$10cm$的小正方形。
裁剪示意图中,在长方形纸片的四个角分别画边长为$10cm$的正方形(用实线表示剪切线),然后将四周的纸片向上折起(用虚线表示折痕),并标出相应尺寸。图略。
(2) 剪去四个角的小正方形后,折成的无盖长方体盒子底面是一个长为$(40 - 2×10)cm$,宽为$(30 - 2×10)cm$的长方形,高为$10cm$。
根据长方体容积公式$V = 长×宽×高$,可求出盒子的容积。
【答案】:
(1)如图所示
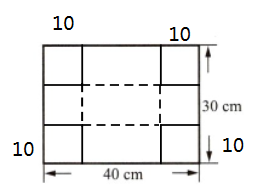
(2)盒子底面长为:$40 - 2×10 = 20$($cm$);
盒子底面宽为:$30 - 2×10 = 10$($cm$);
盒子容积$V = 20×10×10 = 2000$($cm^3$)。
所以该盒子的容积为$2000cm^3$。
【解析】:
本题主要考查长方体的展开图及容积计算。
(1)因为要折成一个高为$10cm$的无盖长方体盒子,所以在长方形纸片的四个角各剪去一个边长为$10cm$的小正方形。
裁剪示意图中,在长方形纸片的四个角分别画边长为$10cm$的正方形(用实线表示剪切线),然后将四周的纸片向上折起(用虚线表示折痕),并标出相应尺寸。图略。
(2) 剪去四个角的小正方形后,折成的无盖长方体盒子底面是一个长为$(40 - 2×10)cm$,宽为$(30 - 2×10)cm$的长方形,高为$10cm$。
根据长方体容积公式$V = 长×宽×高$,可求出盒子的容积。
【答案】:
(1)如图所示

(2)盒子底面长为:$40 - 2×10 = 20$($cm$);
盒子底面宽为:$30 - 2×10 = 10$($cm$);
盒子容积$V = 20×10×10 = 2000$($cm^3$)。
所以该盒子的容积为$2000cm^3$。
查看更多完整答案,请扫码查看


