第121页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
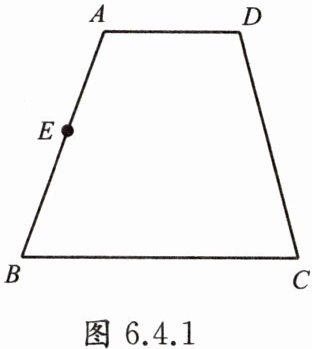
例1 如图6.4.1,AD//BC,点E在AB上.
(1)过点E画BC的平行线,交CD于点F;
(2)观察EF和AD的位置关系,并用直尺和三角板加以验证,由此可得到怎样的猜想?
(1)过点E画BC的平行线,交CD于点F;
(2)观察EF和AD的位置关系,并用直尺和三角板加以验证,由此可得到怎样的猜想?

答案:
(1) 解:作图步骤:把三角板的一条直角边与BC重合,用直尺紧靠三角板的另一条直角边,沿直尺移动三角板,使三角板与BC重合的直角边过点E,过点E沿三角板的直角边画直线,交CD于点F,EF即为所求。
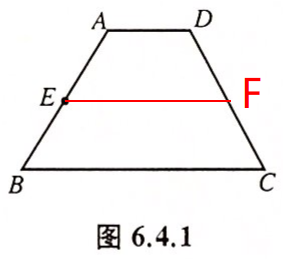
(2) 解:EF和AD的位置关系是平行。
验证:用三角板的一条直角边与AD重合,另一条直角边与直尺重合,沿直尺平移三角板,观察到三角板与AD重合的直角边能与EF重合,说明EF//AD。
猜想:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
(1) 解:作图步骤:把三角板的一条直角边与BC重合,用直尺紧靠三角板的另一条直角边,沿直尺移动三角板,使三角板与BC重合的直角边过点E,过点E沿三角板的直角边画直线,交CD于点F,EF即为所求。

(2) 解:EF和AD的位置关系是平行。
验证:用三角板的一条直角边与AD重合,另一条直角边与直尺重合,沿直尺平移三角板,观察到三角板与AD重合的直角边能与EF重合,说明EF//AD。
猜想:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
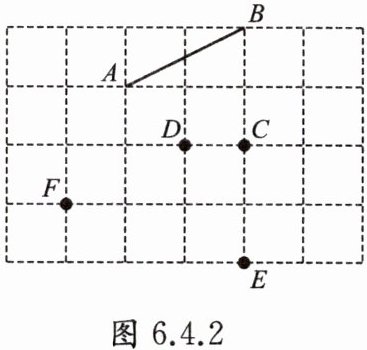
例2 如图6.4.2,在6×4的正方形网格中,点A,B,C,D,E,F都在格点上.连接点A,B,得线段AB.
(1)连接C,D,E,F中的任意两点,共可得______条线段,在图中画出来;
(2)在(1)中所连得的线段中,与AB平行的线段是______,用符号表示:______;
(3)过点D画AB的平行线,只能画______条直线,理由是______.
(1)连接C,D,E,F中的任意两点,共可得______条线段,在图中画出来;
(2)在(1)中所连得的线段中,与AB平行的线段是______,用符号表示:______;
(3)过点D画AB的平行线,只能画______条直线,理由是______.

答案:
【解析】:
(1) 从$C,D,E,F$中任取两点,可得线段$CD$, $CE$, $CF$, $DE$, $DF$, $EF$,共6条。
(2) 观察图形,我们可以发现线段$DF$与$AB$在网格中形成了相同的倾斜角度,因此$DF// AB$,用符号表示为$AB// DF$。
(3) 根据平行公理,经过直线外一点(即点D),有且只有一条直线与该直线平行。
【答案】:
(1) 6;
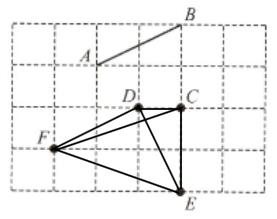
(2) $DF$;$AB// DF$
(3) 1;经过直线外一点,有且只有一条直线与已知直线平行
【解析】:
(1) 从$C,D,E,F$中任取两点,可得线段$CD$, $CE$, $CF$, $DE$, $DF$, $EF$,共6条。
(2) 观察图形,我们可以发现线段$DF$与$AB$在网格中形成了相同的倾斜角度,因此$DF// AB$,用符号表示为$AB// DF$。
(3) 根据平行公理,经过直线外一点(即点D),有且只有一条直线与该直线平行。
【答案】:
(1) 6;

(2) $DF$;$AB// DF$
(3) 1;经过直线外一点,有且只有一条直线与已知直线平行
1. 若C是直线AB外的一点,则下列说法正确的是(
A.过点C可以画两条直线与直线AB平行
B.过点C有且只有一条直线与直线AB平行
C.过点C不能画直线与直线AB平行
D.过点C有无数条直线与直线AB平行
B
)A.过点C可以画两条直线与直线AB平行
B.过点C有且只有一条直线与直线AB平行
C.过点C不能画直线与直线AB平行
D.过点C有无数条直线与直线AB平行
答案:
【解析】:
这个问题考查的是平行线的定义和性质。根据平行线的定义,通过直线外的一个点,有且仅有一条直线与该直线平行。
A选项:说过点C可以画两条直线与直线AB平行,这与平行线的性质相矛盾,因为通过点C只能画一条与AB平行的直线。
B选项:表示过点C有且只有一条直线与直线AB平行,这符合平行线的性质。
C选项:说过点C不能画直线与直线AB平行,这是错误的,因为根据平行线的性质,我们可以过点C画一条与AB平行的直线。
D选项:说过点C有无数条直线与直线AB平行,这也是错误的,因为通过点C只能画一条与AB平行的直线。
综上所述,只有B选项是正确的。
【答案】:
B
这个问题考查的是平行线的定义和性质。根据平行线的定义,通过直线外的一个点,有且仅有一条直线与该直线平行。
A选项:说过点C可以画两条直线与直线AB平行,这与平行线的性质相矛盾,因为通过点C只能画一条与AB平行的直线。
B选项:表示过点C有且只有一条直线与直线AB平行,这符合平行线的性质。
C选项:说过点C不能画直线与直线AB平行,这是错误的,因为根据平行线的性质,我们可以过点C画一条与AB平行的直线。
D选项:说过点C有无数条直线与直线AB平行,这也是错误的,因为通过点C只能画一条与AB平行的直线。
综上所述,只有B选项是正确的。
【答案】:
B
2. 已知∠AOB,过点P有且只有一条直线与OA平行,则点P(
A.不可能在OB上
B.一定在OA外
C.可能与点O重合
D.一定不在OB上
B
)A.不可能在OB上
B.一定在OA外
C.可能与点O重合
D.一定不在OB上
答案:
解:根据平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
若点P在OB上,当OB与OA不平行时,过点P有且只有一条直线与OA平行;当OB与OA平行时,过点P有无数条直线与OA平行(此时OB上所有点都满足),但题目未说明OA与OB是否平行,所以点P可能在OB上,A、D错误。
若点P与点O重合,过点O有且只有一条直线与OA平行(OA本身不符合平行定义,应为过点O且不与OA重合的直线),但点O在OA上,过直线上一点无法作该直线的平行线,C错误。
点P一定在OA外,因为过直线上一点不能作该直线的平行线,B正确。
答案:B
若点P在OB上,当OB与OA不平行时,过点P有且只有一条直线与OA平行;当OB与OA平行时,过点P有无数条直线与OA平行(此时OB上所有点都满足),但题目未说明OA与OB是否平行,所以点P可能在OB上,A、D错误。
若点P与点O重合,过点O有且只有一条直线与OA平行(OA本身不符合平行定义,应为过点O且不与OA重合的直线),但点O在OA上,过直线上一点无法作该直线的平行线,C错误。
点P一定在OA外,因为过直线上一点不能作该直线的平行线,B正确。
答案:B
3. 在同一平面内,不重合的两条直线可能的位置关系是
相交或平行
.
答案:
【解析】:
本题考查的是同一平面内两条不重合直线的位置关系。在同一平面内,两条不重合的直线只有两种可能的位置关系:一是它们相交于某一点,二是它们始终保持相同的距离,即平行。
【答案】:
相交或平行
本题考查的是同一平面内两条不重合直线的位置关系。在同一平面内,两条不重合的直线只有两种可能的位置关系:一是它们相交于某一点,二是它们始终保持相同的距离,即平行。
【答案】:
相交或平行
查看更多完整答案,请扫码查看


