《2025年课课练江苏七年级数学上册苏科版》

1. $1与-2025$的差是(D)
A.$-2026$
B.$2024$
C.$-2024$
D.$2026$

答案： 解：根据题意，1与-2025的差可表示为$1 - (-2025)$。
依据有理数减法法则：减去一个数等于加上这个数的相反数，可得：
$1 - (-2025) = 1 + 2025 = 2026$
答案：D

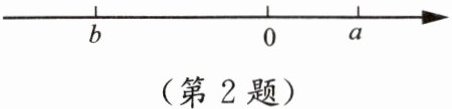
2. 有理数$a,b$在数轴上的位置如图所示,有下列结论：①$a+b＜0$；②$a-b＜0$；③$a＜|b|$；④$-a＞-b$；⑤$|a-b|= a-b$.其中正确的有(C)

A.$2$个
B.$3$个
C.$4$个
D.$5$个

答案： 解：由数轴知：$b ＜ 0 ＜ a$，且$|b| ＞ |a|$。
① $a + b ＜ 0$（异号两数相加，取绝对值较大的符号，$|b| ＞ |a|$，故和为负），正确；
② $a - b = a + (-b) ＞ 0$（$-b ＞ 0$，正数加正数为正），则$a - b ＜ 0$错误；
③ $|b| ＞ |a|$且$a ＞ 0$，则$a ＜ |b|$，正确；
④ $a ＜ |b| = -b$，则$-a ＞ -b$（不等式两边乘$-1$，不等号方向改变），正确；
⑤ $a - b ＞ 0$，则$|a - b| = a - b$，正确。
综上，正确的有①③④⑤，共4个。
答案：C

3. 直接填写计算结果：
(1)$4-8= $$-4$；
(2)$4-(-8)= $$12$；
(3)$(-4)-8= $$-12$；
(4)$(-4)-(-8)= $$4$；
(5)$0-8= $$-8$；
(6)$0-(-8)= $$8$.

答案： 【解析】：
题目考查的是有理数的减法运算规则。
(1) 对于 $4-8$，直接进行减法运算。
(2) 对于 $4-(-8)$，根据减法运算法则，减去负数等于加上这个数的绝对值，即 $4+8$。
(3) 对于 $(-4)-8$，直接进行减法运算，即 $-4$ 加上 $-8$。
(4) 对于 $(-4)-(-8)$，根据减法运算法则，减去负数等于加上这个数的绝对值，即 $-4+8$。
(5) 对于 $0-8$，直接进行减法运算。
(6) 对于 $0-(-8)$，根据减法运算法则，减去负数等于加上这个数的绝对值，即 $0+8$。
【答案】：
(1) $-4$
(2) $12$
(3) $-12$
(4) $4$
(5) $-8$
(6) $8$

4. 填空：
(1)$(-6)+$21$=15$；
(2)$23+$-27$=-4$；
(3)3$-(-21)= 24$.

答案： 【解析】：
本题主要考察有理数的加减法运算。
(1) 对于$(-6)+$______$=15$，我们需要找到一个数，与-6相加得到15。
设这个数为x，则有$-6 + x = 15$，解得$x = 21$。
(2) 对于$23+$______$=-4$，我们需要找到一个数，与23相加得到-4。
设这个数为y，则有$23 + y = -4$，解得$y = -27$。
(3) 对于______$-(-21)= 24$，我们需要找到一个数，减去-21（即加上21）得到24。
设这个数为z，则有$z + 21 = 24$，解得$z = 3$。
【答案】：
(1) 21
(2) -27
(3) 3

5. 如图是一台冰箱的显示屏,则这台冰箱冷藏室与冷冻室的温差为22°C.

答案： 【解析】：
题目考查有理数的减法在实际问题中的应用。
要求冷藏室与冷冻室的温差，需要用冷藏室的温度减去冷冻室的温度，根据有理数减法法则，减去一个数等于加上这个数的相反数来计算。
【答案】：
解：已知冷藏室温度为$4^{\circ}C$，冷冻室温度为$-18^{\circ}C$，则温差为：
$4 - (-18)=4 + 18 = 22(^{\circ}C)$
故答案为$22$。

6. 计算：
(1)$(-37)-(-47)$；
(2)$(-53)-16$；
(3)$(-210)-87$；
(4)$1.3-(-2.7)$.

答案： 【解析】：
本题主要考察有理数的加减法运算。对于有理数的减法，可以转化为加法进行计算，即减去一个数等于加上这个数的相反数。
(1) 对于$(-37)-(-47)$，可以转化为$(-37)+47$；
(2) 对于$(-53)-16$，可以转化为$(-53)+(-16)$；
(3) 对于$(-210)-87$，可以转化为$(-210)+(-87)$；
(4) 对于$1.3-(-2.7)$，可以转化为$1.3+2.7$。
【答案】：
(1) 解：
$(-37)-(-47)$
$= (-37)+47$
$= 10$
(2) 解：
$(-53)-16$
$= (-53)+(-16)$
$= -69$
(3) 解：
$(-210)-87$
$= (-210)+(-87)$
$= -297$
(4) 解：
$1.3-(-2.7)$
$= 1.3+2.7$
$= 4$

7. 小明在计算$-3.25-■$后,不小心将墨水滴在减数位置.若他在计算过程中误将$-3.25$后面的“$-$”看成了“$+$”,从而算得结果为$5\frac{3}{4}$,请求出被墨水污染的减数,并正确计算此道题.

答案： 【解析】：
此题主要考查了有理数的加减法运算。
首先，我们需要根据小明的错误计算，推算出被墨水污染的减数。
然后，我们再用正确的运算符号“-”，求出正确的结果。
设被墨水污染的减数为$x$，
根据小明的错误计算，我们可以列出方程：
$-3.25 + x = 5\frac{3}{4}$
将$5\frac{3}{4}$转换为小数，即$5.75$，代入方程得：
$-3.25 + x = 5.75$
解这个方程，我们可以得到：
$x = 5.75 + 3.25 = 9$
所以，被墨水污染的减数是$9$。
接下来，我们用正确的运算符号“-”，计算原式的结果：
$-3.25 - 9 = -12.25$
【答案】：
被墨水污染的减数是$9$，正确的计算结果是$-12.25$。