第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
1. 在下面的月历中,任意圈出一竖列上相邻的三个数,这三个数之和不可能为 (
A.75
B.60
C.36
D.27
A
)A.75
B.60
C.36
D.27
答案:
解:设中间的数为$x$,则上面的数为$x - 7$,下面的数为$x + 7$。
三个数之和为:$(x - 7) + x + (x + 7) = 3x$,即三个数之和是$3$的倍数。
A. $75÷3 = 25$,中间数为$25$,上面数为$25 - 7 = 18$,下面数为$25 + 7 = 32$。月历中最大数为$31$,$32$不存在,所以不可能。
B. $60÷3 = 20$,中间数$20$,上面$13$,下面$27$,存在。
C. $36÷3 = 12$,中间数$12$,上面$5$,下面$19$,存在。
D. $27÷3 = 9$,中间数$9$,上面$2$,下面$16$,存在。
答案:A
三个数之和为:$(x - 7) + x + (x + 7) = 3x$,即三个数之和是$3$的倍数。
A. $75÷3 = 25$,中间数为$25$,上面数为$25 - 7 = 18$,下面数为$25 + 7 = 32$。月历中最大数为$31$,$32$不存在,所以不可能。
B. $60÷3 = 20$,中间数$20$,上面$13$,下面$27$,存在。
C. $36÷3 = 12$,中间数$12$,上面$5$,下面$19$,存在。
D. $27÷3 = 9$,中间数$9$,上面$2$,下面$16$,存在。
答案:A
2. 某街道分布示意图如图所示,一个居民从A处前往B处,若规定只能从左到右或从上到下的方向,这样该居民共有可选择的不同路线条数是 (
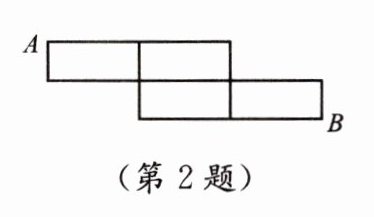
A.6
B.7
C.8
D.9
C
)
A.6
B.7
C.8
D.9
答案:
C
3. 由3,7,0,6四个数字可以组成
18
个不同的四位数,其中最大的四位数是7630
.
答案:
解:千位数字不能为0,分情况讨论:
1. 千位为3:剩余数字0,6,7,可组成3067,3076,3607,3670,3706,3760,共6个;
2. 千位为6:剩余数字0,3,7,可组成6037,6073,6307,6370,6703,6730,共6个;
3. 千位为7:剩余数字0,3,6,可组成7036,7063,7306,7360,7603,7630,共6个。
不同四位数总数:6+6+6=18个。
最大四位数:7630。
18;7630
1. 千位为3:剩余数字0,6,7,可组成3067,3076,3607,3670,3706,3760,共6个;
2. 千位为6:剩余数字0,3,7,可组成6037,6073,6307,6370,6703,6730,共6个;
3. 千位为7:剩余数字0,3,6,可组成7036,7063,7306,7360,7603,7630,共6个。
不同四位数总数:6+6+6=18个。
最大四位数:7630。
18;7630
4. 如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,该无盖长方体盒子的容积是
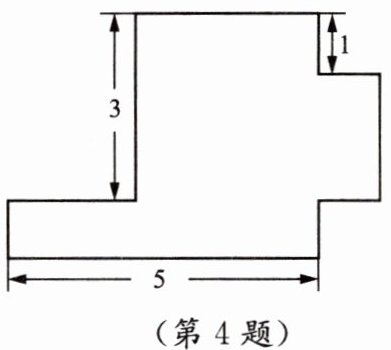
单位:cm
6
$cm^3.$
单位:cm
答案:
【解析】:
本题可根据长方体展开图求出长方体的长、宽、高,再根据长方体容积公式进行计算,考查了长方体展开图与长方体各部分的关系以及长方体容积的计算方法。
从展开图可知,长方体的高为$1cm$;
底面长方形的长为$5 - 1 - 1 = 3cm$(因为两个高组成了减去的部分);
宽为$3 - 1 = 2cm$(总长度减去高得到宽)。
根据长方体容积公式$V = 长×宽×高$,可求出该无盖长方体盒子的容积。
【答案】:
解:由展开图可知,长方体的高$h = 1cm$,底面长方形的长$a = 5 - 1 - 1 = 3cm$,宽$b = 3 - 1 = 2cm$。
根据长方体容积公式$V = a× b× h$,可得:
$V = 3×2×1 = 6(cm^3)$
故答案为:$6$。
本题可根据长方体展开图求出长方体的长、宽、高,再根据长方体容积公式进行计算,考查了长方体展开图与长方体各部分的关系以及长方体容积的计算方法。
从展开图可知,长方体的高为$1cm$;
底面长方形的长为$5 - 1 - 1 = 3cm$(因为两个高组成了减去的部分);
宽为$3 - 1 = 2cm$(总长度减去高得到宽)。
根据长方体容积公式$V = 长×宽×高$,可求出该无盖长方体盒子的容积。
【答案】:
解:由展开图可知,长方体的高$h = 1cm$,底面长方形的长$a = 5 - 1 - 1 = 3cm$,宽$b = 3 - 1 = 2cm$。
根据长方体容积公式$V = a× b× h$,可得:
$V = 3×2×1 = 6(cm^3)$
故答案为:$6$。
5. 某商店甲、乙两种商品的进货价不同,根据市场行情,商店调整了售价,调整后的售价均为240元.按此计算,甲商品每件赢利20%,乙商品每件亏损20%,调整后该商店卖出甲、乙两种商品各10件,问该商店是赚钱还是赔钱?赚了(或赔了)多少?
答案:
解:设甲商品的进货价为$x$元,乙商品的进货价为$y$元。
甲商品:$(1 + 20\%)x = 240$
$1.2x = 240$
$x = 200$
乙商品:$(1 - 20\%)y = 240$
$0.8y = 240$
$y = 300$
甲商品每件利润:$240 - 200 = 40$(元)
乙商品每件亏损:$300 - 240 = 60$(元)
各卖10件总利润:$10×40 - 10×60 = 400 - 600 = -200$(元)
答:该商店赔钱,赔了200元。
甲商品:$(1 + 20\%)x = 240$
$1.2x = 240$
$x = 200$
乙商品:$(1 - 20\%)y = 240$
$0.8y = 240$
$y = 300$
甲商品每件利润:$240 - 200 = 40$(元)
乙商品每件亏损:$300 - 240 = 60$(元)
各卖10件总利润:$10×40 - 10×60 = 400 - 600 = -200$(元)
答:该商店赔钱,赔了200元。
6. 定义新运算“△”,规定a△b= 4×a+3×b+1.
(1) 5△7和7△5的值相等吗?
(2) 对于两个自然数a和b,若a△b= b△a,则a和b有什么关系?
(3) 运算“△”满足交换律吗?
(1) 5△7和7△5的值相等吗?
(2) 对于两个自然数a和b,若a△b= b△a,则a和b有什么关系?
(3) 运算“△”满足交换律吗?
答案:
【解析】:
本题主要考查自定义运算的理解与应用,以及代数式的化简和等式的求解。
(1) 根据定义,我们可以直接代入数值进行计算。
(2) 需要根据给定的等式进行化简和求解,找出a和b之间的关系。
(3) 通过对比a△b和b△a的表达式,判断它们是否总是相等,从而确定运算“△”是否满足交换律。
【答案】:
(1)
解:根据定义,我们有
$5\bigtriangleup7 = 4 × 5 + 3 × 7 + 1 = 20 + 21 + 1 = 42$
$7\bigtriangleup5 = 4 × 7 + 3 × 5 + 1 = 28 + 15 + 1 = 44$
由于 $42 \neq 44$,所以 $5\bigtriangleup7$ 和 $7\bigtriangleup5$ 的值不相等。
(2)
解:根据题意,我们有
$a\bigtriangleup b = 4a + 3b + 1$
$b\bigtriangleup a = 4b + 3a + 1$
由 $a\bigtriangleup b = b\bigtriangleup a$,我们得到
$4a + 3b + 1 = 4b + 3a + 1$
化简得:
$a = b$
所以,当 $a\bigtriangleup b = b\bigtriangleup a$ 时,$a$ 和 $b$ 必须相等。
(3)
解:运算“$\bigtriangleup$”不满足交换律。
由
(2)的解答过程,我们知道只有当 $a = b$ 时,$a\bigtriangleup b$ 才等于 $b\bigtriangleup a$。
对于 $a \neq b$ 的情况,$a\bigtriangleup b$ 和 $b\bigtriangleup a$ 的值是不相等的。
因此,运算“$\bigtriangleup$”不满足交换律。
本题主要考查自定义运算的理解与应用,以及代数式的化简和等式的求解。
(1) 根据定义,我们可以直接代入数值进行计算。
(2) 需要根据给定的等式进行化简和求解,找出a和b之间的关系。
(3) 通过对比a△b和b△a的表达式,判断它们是否总是相等,从而确定运算“△”是否满足交换律。
【答案】:
(1)
解:根据定义,我们有
$5\bigtriangleup7 = 4 × 5 + 3 × 7 + 1 = 20 + 21 + 1 = 42$
$7\bigtriangleup5 = 4 × 7 + 3 × 5 + 1 = 28 + 15 + 1 = 44$
由于 $42 \neq 44$,所以 $5\bigtriangleup7$ 和 $7\bigtriangleup5$ 的值不相等。
(2)
解:根据题意,我们有
$a\bigtriangleup b = 4a + 3b + 1$
$b\bigtriangleup a = 4b + 3a + 1$
由 $a\bigtriangleup b = b\bigtriangleup a$,我们得到
$4a + 3b + 1 = 4b + 3a + 1$
化简得:
$a = b$
所以,当 $a\bigtriangleup b = b\bigtriangleup a$ 时,$a$ 和 $b$ 必须相等。
(3)
解:运算“$\bigtriangleup$”不满足交换律。
由
(2)的解答过程,我们知道只有当 $a = b$ 时,$a\bigtriangleup b$ 才等于 $b\bigtriangleup a$。
对于 $a \neq b$ 的情况,$a\bigtriangleup b$ 和 $b\bigtriangleup a$ 的值是不相等的。
因此,运算“$\bigtriangleup$”不满足交换律。
查看更多完整答案,请扫码查看


