《2025年课课练江苏七年级数学上册苏科版》

1. 下列赋予整式$ 8a $实际意义的例子中,错误的是(C)
A.长为8,宽为$ a $的长方形的面积
B.货车以$ a \ km/h $的平均速度行驶8h的路程
C.原价为$ a $元的商品打8折后的售价
D.购买8本单价为$ a $元的笔记本所需的费用

答案： 【解析】：
本题主要考察整式的实际意义，需要判断各个选项是否与整式$8a$相符合。
A选项表示长方形的面积，长为8，宽为$a$，根据长方形面积公式：面积=长$×$宽，即$8 × a = 8a$，与整式$8a$相符，所以A选项正确。
B选项表示货车行驶的路程，平均速度为$a \ km/h$，行驶时间为8h，根据路程公式：路程=速度$×$时间，即$a × 8 = 8a$，与整式$8a$相符，所以B选项正确。
C选项表示商品打折后的售价，原价为$a$元，打8折后的售价应为$0.8a$，与整式$8a$不符，所以C选项错误。
D选项表示购买笔记本的费用，单价为$a$元，购买数量为8本，根据费用公式：费用=单价$×$数量，即$a × 8 = 8a$，与整式$8a$相符，所以D选项正确。
综上所述，错误的选项是C。
【答案】：C

2. 已知一个两位数的十位数字是3,个位数字是$ a $,用式子表示这个两位数是(D)
A.$ 3a $
B.$ 30a $
C.$ 3+a $
D.$ 30+a $

答案： 解：两位数的表示方法为：十位数字×10 + 个位数字。
已知十位数字是3，个位数字是a，
则这个两位数可表示为：3×10 + a = 30 + a。
答案：D

3. 试写出一个含$ x $的式子：$- x^{2} - 1$（答案不唯一）,使$ x $不论取何值,这个式子的值总是负数.

答案： 【解析】：
本题主要考查字母表示数以及如何构造一个恒为负数的代数式。
考虑到任何数的平方都是非负的，即$x^2 \geq 0$，那么$-x^2$就会恒小于等于0，即$-x^2 \leq 0$。
为了使式子恒为负数，我们只需要在$-x^2$的基础上再减去一个正数，比如1，得到$-x^2 - 1$。
这样，无论$x$取何值，$-x^2 - 1$都会小于0，即恒为负数。
【答案】：
$- x^{2} - 1$（答案不唯一）

4. 等腰三角形的周长为8,若它的底边长为$ a $,则腰长为$4 - \frac{a}{2}$.

答案： 【解析】：
本题考查等腰三角形的性质以及代数式的表示。
等腰三角形的两腰相等，设腰长为$b$，底边长为$a$。
根据等腰三角形的周长公式，有：
$2b + a = 8$
从上式中解出$b$，得到：
$b = \frac{8 - a}{2} = 4 - \frac{a}{2}$
【答案】：
$4 - \frac{a}{2}$

5. 用字母表示下列运算或数量关系：
(1)一个数的4倍与另一个数的差；$4a - b$
(2)两数之和与这两数之差的商；$\frac{a+b}{a-b}$（$a \neq b$）
(3)某数的$\frac{1}{2}与它的\frac{1}{3}$的和等于5；$\frac{1}{2}x + \frac{1}{3}x = 5$
(4)一个数的2倍减3后小于它的3倍.$2x - 3 ＜ 3x$

答案： 【解析】：
本题主要考查用字母表示数以及代数式的书写。
(1) 设一个数为$a$，另一个数为$b$，则这个数的4倍与另一个数的差可以表示为$4a - b$。
(2) 设两个数为$a$和$b$，则两数之和为$a+b$，两数之差为$a-b$（或$b-a$，但通常我们取$a-b$为正差），所以两数之和与这两数之差的商可以表示为$\frac{a+b}{a-b}$（注意$a \neq b$）。
(3) 设某数为$x$，则它的$\frac{1}{2}$为$\frac{1}{2}x$，它的$\frac{1}{3}$为$\frac{1}{3}x$，根据题意，这两者的和等于5，所以可以表示为方程：$\frac{1}{2}x + \frac{1}{3}x = 5$。
(4) 设一个数为$x$，则它的2倍为$2x$，它的3倍为$3x$，根据题意，这个数的2倍减3后小于它的3倍，所以可以表示为不等式：$2x - 3 ＜ 3x$。
【答案】：
(1) $4a - b$
(2) $\frac{a+b}{a-b}$（$a \neq b$）
(3) $\frac{1}{2}x + \frac{1}{3}x = 5$
(4) $2x - 3 ＜ 3x$

6. 在小学,我们学过简便运算,如$ 5×6+3×6= (5+3)×6= 48 $.请回答下列问题：
(1)上面的简便运算运用的运算律是什么？用字母表示出来.
乘法分配律，$a×(b+c) = a× b + a× c$
(2)运用上面的方法,可以得到$ 3x+5x $的结果是______.8x

答案： 【解析】：
(1) 这个问题考查的是对乘法分配律的理解和应用。乘法分配律是指两个数的和同一个数相乘，等于把两个加数分别同这个数相乘，再把两个积加起来，结果不变。用字母表示就是$a×(b+c) = a× b + a× c$。
(2) 这个问题考查的是对乘法分配律的逆向应用。当我们看到$3x+5x$时，可以把它看作是两个项的和，每个项都含有一个公共的因子$x$，因此我们可以把它写成$(3+5)× x$，进一步简化得到$8x$。
【答案】：
(1) 运用的运算律是乘法分配律，用字母表示出来为：$a×(b+c) = a× b + a× c$。
(2) $3x+5x$的结果是$8x$。

7. 如图所示的图形都由同样大小的小圆圈按一定规律组成,按此规律排列下去,请用含$ n 的代数式表示第 n $个图形中小圆圈的个数.

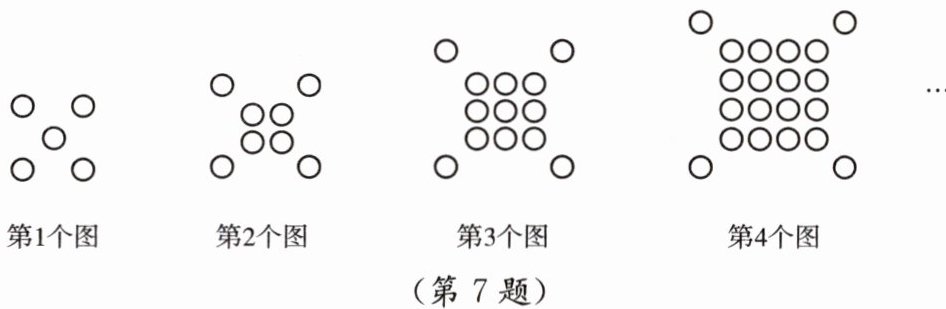
答案： 解：n²+4

8. 如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,请写一条关于$ a,b,c $三个量的等式.

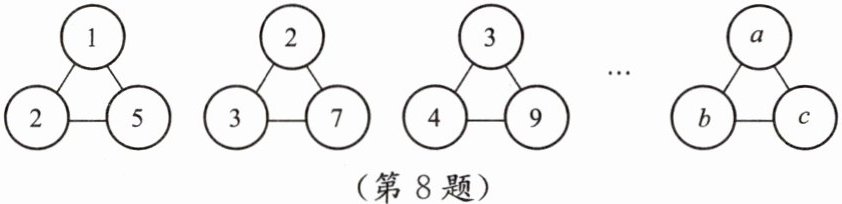
答案： 解：c=3b－a