《2025年课课练江苏七年级数学上册苏科版》

3. $ -(-\frac{2}{3}) $的相反数是$-\frac{2}{3}$；$ -|-\frac{2}{3}| $的相反数是$\frac{2}{3}$.

答案： 解：
$-(-\frac{2}{3})=\frac{2}{3}$，$\frac{2}{3}$的相反数是$-\frac{2}{3}$；
$-|-\frac{2}{3}|=-\frac{2}{3}$，$-\frac{2}{3}$的相反数是$\frac{2}{3}$。
$-\frac{2}{3}$；$\frac{2}{3}$

4. 把$-5$,$ -(-5) $,$ 0 $,$ |-5.5| $,$ -\frac{1}{5} $这五个数按从大到小,从左到右串成葫芦(数字直接写在圈内).

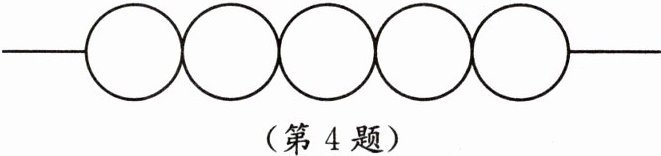
|-5.5|$ -(-5) 0 -\frac{1}{5} -5$

答案： 【解析】：本题考查绝对值，相反数及有理数大小比较。
需要先分别计算出这五个数的具体值，再根据有理数的大小比较规则进行排序。
-5：直接给出，无需计算。
-(-5)：根据相反数的定义，-(-5) = 5。
0：直接给出，无需计算。
|-5.5|：根据绝对值的定义，|-5.5| = 5.5。
$-\frac{1}{5}$：直接给出，无需计算，也可以写成小数形式为-0.2，方便比较大小。
根据有理数的大小比较规则，正数大于0，0大于负数，正数之间或负数之间比较绝对值大小，绝对值大的数反而小，可以得到以下排序：
5.5 ＞ 5 ＞ 0 ＞ -0.2 ＞ -5，
即|-5.5|$ ＞ -(-5) ＞ 0 ＞ -\frac{1}{5} ＞ -5$
最后，将排序后的数串成葫芦形。
【答案】：|-5.5|$ -(-5) 0 -\frac{1}{5} -5。$

5. 若$ |x| 与 |2y - 4| $互为相反数,则$ x= $0,$ y= $2.

答案： 解：因为$|x|$与$|2y - 4|$互为相反数，所以$|x| + |2y - 4| = 0$。
由于绝对值具有非负性，即$|x| \geq 0$，$|2y - 4| \geq 0$，要使两个非负数的和为$0$，则这两个非负数必须都为$0$。
所以$|x| = 0$，解得$x = 0$；$|2y - 4| = 0$，即$2y - 4 = 0$，解得$y = 2$。
$x = 0$，$y = 2$

6. 化简：
(1)$ -(-3) $； (2)$ -|-3.2| $； (3)$ +(-0.5) $； (4)$ -|+\frac{1}{3}| $.

答案： 【解析】：
本题主要考查了相反数和绝对值的定义及其性质。
(1) 对于 $-(-3)$，根据相反数的定义，负负得正，所以 $-(-3) = 3$。
(2) 对于 $-|-3.2|$，首先根据绝对值的定义，$|-3.2| = 3.2$，再取其相反数，即 $-3.2$。
(3) 对于 $+(-0.5)$，根据正负数的性质，正号对负数无影响，所以 $+(-0.5) = -0.5$。
(4) 对于 $-|+\frac{1}{3}|$，首先根据绝对值的定义，$|+\frac{1}{3}| = \frac{1}{3}$，再取其相反数，即 $-\frac{1}{3}$。
【答案】：
(1) $3$
(2) $-3.2$
(3) $-0.5$
(4) $-\frac{1}{3}$

7. 比较下列每组数的大小：
(1)$ -2 和 +6 $； (2)$ 0 和 -1.8 $； (3)$ -\frac{3}{2} 和 -4 $.

答案： 【解析】：
本题主要考查了有理数的大小比较，特别是负数与正数，负数与负数之间的比较。
对于第一组数，$-2$是负数，$+6$是正数，根据有理数大小比较的规则，正数总是大于负数，所以$-2 ＜ +6$。
对于第二组数，$0$是非负数，$-1.8$是负数，根据有理数大小比较的规则，非负数总是大于负数，所以$0 ＞ -1.8$。
对于第三组数，$-\frac{3}{2}$和$-4$都是负数，根据有理数大小比较的规则，绝对值大的负数反而小，所以我们需要比较它们的绝对值。
$\left|-\frac{3}{2}\right| = \frac{3}{2} = 1.5$，$\left|-4\right| = 4$，因为$1.5 ＜ 4$，所以$-\frac{3}{2} ＞ -4$。
【答案】：
(1) $-2 ＜ +6$
(2) $0 ＞ -1.8$
(3) $-\frac{3}{2} ＞ -4$

8. 如果$ a$,$ b $都是有理数,且$ a ＞ b $,那么$ |a| 一定大于 |b| $吗？如果$ |a| ＞ |b| $,那么$ a 一定大于 b $吗？举例说明.

答案： 解：如果$a$，$b$都是有理数，且$a ＞ b$，那么$|a|$不一定大于$|b|$。
举例：设$a = 1$，$b=-2$，满足$a ＞ b$，但$|a|=1$，$|b|=2$，此时$|a| ＜ |b|$。
如果$|a| ＞ |b|$，那么$a$不一定大于$b$。
举例：设$a=-3$，$b=1$，满足$|a|=3 ＞ |b|=1$，但$a=-3 ＜ b=1$。
结论：$a ＞ b$时$|a|$不一定大于$|b|$；$|a| ＞ |b|$时$a$不一定大于$b$。

9. 如果实际值为$ a $,测量值为$ b $,那么我们把$ |a - b| $称为绝对误差,$ \frac{|a - b|}{a} $称为相对误差.若有一种零件实际长度为$ 5.0\ cm $,测量得$ 4.8\ cm $,则测量所产生的绝对误差是0.2$ cm $,相对误差是0.04$ cm $.

答案： 【解析】：
题目考查了绝对误差和相对误差的计算。
绝对误差是测量值与实际值之差的绝对值，即 $|a - b|$。
相对误差是绝对误差与实际值的比值，即 $\frac{|a - b|}{a}$。
根据题目，实际值 $a = 5.0 cm$，测量值 $b = 4.8 cm$。
首先计算绝对误差：
$|a - b| = |5.0 - 4.8| = 0.2 cm$
然后计算相对误差：
$\frac{|a - b|}{a} = \frac{0.2}{5.0} = 0.04$
但注意，相对误差通常不带有单位，因为它是一个比值。
所以，相对误差应表述为 $0.04$（或写作 $4\%$，但题目中要求的是小数形式，所以应为 $0.04$）。
【答案】：
绝对误差是 $0.2 cm$，相对误差是 $0.04$。

10. 已知甲数的绝对值是乙数绝对值的2倍,且在数轴上表示甲、乙两数的两点之间的距离是9.
(1)若表示甲、乙两数的两点位于原点的两侧,求这两个数；
(2)若表示甲、乙两数的两点位于原点的同侧,求这两个数.

答案：
(1)设乙数的绝对值为$x$，则甲数的绝对值为$2x$。
因为甲、乙两数的两点位于原点两侧，所以两数异号。
当甲数为正，乙数为负时，甲数为$2x$，乙数为$-x$，两点距离为$2x - (-x)=3x = 9$，解得$x = 3$，则甲数为$6$，乙数为$-3$。
当甲数为负，乙数为正时，甲数为$-2x$，乙数为$x$，两点距离为$x - (-2x)=3x = 9$，解得$x = 3$，则甲数为$-6$，乙数为$3$。
所以这两个数为$6$和$-3$或$-6$和$3$。
(2)设乙数的绝对值为$x$，则甲数的绝对值为$2x$。
因为甲、乙两数的两点位于原点同侧，所以两数同号。
当两数都为正时，甲数为$2x$，乙数为$x$，两点距离为$2x - x = x = 9$，解得$x = 9$，则甲数为$18$，乙数为$9$。
当两数都为负时，甲数为$-2x$，乙数为$-x$，两点距离为$-x - (-2x)=x = 9$，解得$x = 9$，则甲数为$-18$，乙数为$-9$。
所以这两个数为$18$和$9$或$-18$和$-9$。