《2025年课课练江苏七年级数学上册苏科版》

例 1 当$a= -1$,$b= 2$时,求下列代数式的值：
(1)$a^{2}-2ab+b^{2}$；
(2)$(a-b)^{2}$；
(3)$\frac{1}{a}+\frac{1}{b}$.

答案： 解：
(1) 当$a = -1$，$b = 2$时，
$a^{2}-2ab + b^{2}=(-1)^{2}-2×(-1)×2 + 2^{2}=1 + 4 + 4 = 9$；
(2) 当$a = -1$，$b = 2$时，
$(a - b)^{2}=(-1 - 2)^{2}=(-3)^{2}=9$；
(3) 当$a = -1$，$b = 2$时，
$\frac{1}{a}+\frac{1}{b}=\frac{1}{-1}+\frac{1}{2}=-1+\frac{1}{2}=-\frac{1}{2}$。

例 2 某校羽毛球队需要购买 10 副羽毛球拍和$x盒羽毛球(x＞10)$,羽毛球拍市场价为200 元/副,羽毛球为 30 元/盒,以下是本地两家商场提供的方案：
① 甲商场方案为所有商品九折.
② 乙商场方案为买 1 副羽毛球拍送 1 盒羽毛球,其余原价销售.
请你根据两家商场提供的方案回答下列问题：
(1)分别用含$x$的代数式表示在甲商场和乙商场购买所有物品的费用.
(2)当$x= 20$时,请通过计算说明选择哪个商场购买比较省钱.

答案： 【解析】：
本题主要考查代数式的建立和代数式的求值。
(1)部分需要根据题目描述，利用代数式表示在甲、乙两个商场的购买费用。在甲商场，所有商品都有九折优惠，所以费用为$0.9 × (200 × 10 + 30x)$；在乙商场，买一副羽毛球拍送一盒羽毛球，所以费用为$200 × 10 + 30(x-10)$（因为买了10副羽毛球拍，所以会送10盒羽毛球，故只需为超出的部分付费）。
(2)部分需要将$x=20$代入到前面得到的两个代数式中，计算出在两个商场的具体购买费用，并进行比较。
【答案】：
(1)解：
甲商场的费用为：
$0.9 × (200 × 10 + 30x) = 0.9 × (2000 + 30x) = 1800 + 27x$
乙商场的费用为：
$200 × 10 + 30(x - 10) = 2000 + 30x - 300 = 1700 + 30x$
(2)当$x = 20$时，
甲商场的费用为：
$1800 + 27 × 20 = 1800 + 540 = 2340 (元]$
乙商场的费用为：
$1700 + 30 × 20 = 1700 + 600 = 2300 (元]$
因为2300元 ＜ 2340元，所以选择乙商场购买更省钱。

例 3 如图 3.2.1,已知正方形$ABCD与正方形BEFG的顶点A$,$B$,$E$在同一直线上,且$AB= a$,$BE= b(b＜a)$.

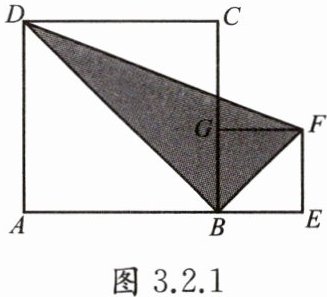
(1)用含$a$,$b$的代数式表示图中阴影部分的面积；
(2)当$a= 5$,$b= 2$时,求图中阴影部分的面积.

答案：

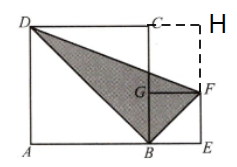
解：$(1)$如图$ $　

　

$S_{阴影}=\frac {1}{2}a²+ab－\frac {1}{2}b²－\frac {1}{2}×(a+b)(a－b) $　　

$=ab $　　

$(2)$当$a=5，$$b=2$时，$S=5×2=10 $　　

1. 已知实数$x$,$y满足|x-1|+(y+2)^{2}= 0$,则代数式$(x+y)^{2025}$的值为(A)
A.$-1$
B.1
C.2025
D.$-2025$

答案： 解：
∵|x-1|+(y+2)²=0，|x-1|≥0，(y+2)²≥0
∴x-1=0，y+2=0
解得x=1，y=-2
∴(x+y)²⁰²⁵=(1-2)²⁰²⁵=(-1)²⁰²⁵=-1
答案：A

2. 已知$a$,$b$互为相反数,$c$,$d$互为倒数,则$(a+b)-cd$的值为(C)
A.0
B.1
C.$-1$
D.2

答案： 解：因为a，b互为相反数，所以a+b=0。
因为c，d互为倒数，所以cd=1。
则(a+b)-cd=0-1=-1。
答案：C