第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
例1 计算:
(1)$(-4)×(-6)$; (2)$(-\frac{1}{2})×\frac{1}{3}$;
(3)$0.5×(-8)$; (4)$(-\frac{2}{3})×(-1)$.
(1)$(-4)×(-6)$; (2)$(-\frac{1}{2})×\frac{1}{3}$;
(3)$0.5×(-8)$; (4)$(-\frac{2}{3})×(-1)$.
答案:
(1)解:$(-4)×(-6)=4×6=24$
(2)解:$(-\frac{1}{2})×\frac{1}{3}=-(\frac{1}{2}×\frac{1}{3})=-\frac{1}{6}$
(3)解:$0.5×(-8)=-(0.5×8)=-4$
(4)解:$(-\frac{2}{3})×(-1)=\frac{2}{3}×1=\frac{2}{3}$
(1)解:$(-4)×(-6)=4×6=24$
(2)解:$(-\frac{1}{2})×\frac{1}{3}=-(\frac{1}{2}×\frac{1}{3})=-\frac{1}{6}$
(3)解:$0.5×(-8)=-(0.5×8)=-4$
(4)解:$(-\frac{2}{3})×(-1)=\frac{2}{3}×1=\frac{2}{3}$
例2 计算:
(1)$(-3.75)×(+3\frac{1}{3})$; (2)$(-1.2)×(+1.5)$;
(3)$(-\frac{7}{3})×(-1\frac{3}{14})$; (4)$2.25×(-\frac{8}{15})$.
(1)$(-3.75)×(+3\frac{1}{3})$; (2)$(-1.2)×(+1.5)$;
(3)$(-\frac{7}{3})×(-1\frac{3}{14})$; (4)$2.25×(-\frac{8}{15})$.
答案:
【解析】:
本题考查了有理数的乘法运算,特别是涉及小数、带分数和真分数的乘法。
解题的关键是掌握有理数乘法的运算法则,即正数乘以正数得正数,负数乘以负数也得正数,而正数乘以负数或负数乘以正数得负数。
同时,要注意将带分数转化为假分数,小数转化为分数进行计算,以便简化运算过程。
【答案】:
(1)
解:
$(-3.75) × (+3\frac{1}{3})$
$= (-\frac{15}{4}) × (\frac{10}{3})$
$= -\frac{150}{12}$
$= -\frac{25}{2}$
或写作 $-12.5$
(2)
解:
$(-1.2) × (+1.5)$
$= (-\frac{6}{5}) × (\frac{3}{2})$
$= -\frac{18}{10}$
$= -\frac{9}{5}$
或写作 $-1.8$
(3)
解:
$(-\frac{7}{3}) × (-1\frac{3}{14})$
$= (-\frac{7}{3}) × (-\frac{17}{14})$
$= \frac{119}{42}$
$= \frac{17}{6}$
或写作 $2\frac{5}{6}$
(4)
解:
$2.25 × (-\frac{8}{15})$
$= (\frac{9}{4}) × (-\frac{8}{15})$
$= -\frac{72}{60}$
$= -\frac{6}{5}$
或写作 $-1.2$
本题考查了有理数的乘法运算,特别是涉及小数、带分数和真分数的乘法。
解题的关键是掌握有理数乘法的运算法则,即正数乘以正数得正数,负数乘以负数也得正数,而正数乘以负数或负数乘以正数得负数。
同时,要注意将带分数转化为假分数,小数转化为分数进行计算,以便简化运算过程。
【答案】:
(1)
解:
$(-3.75) × (+3\frac{1}{3})$
$= (-\frac{15}{4}) × (\frac{10}{3})$
$= -\frac{150}{12}$
$= -\frac{25}{2}$
或写作 $-12.5$
(2)
解:
$(-1.2) × (+1.5)$
$= (-\frac{6}{5}) × (\frac{3}{2})$
$= -\frac{18}{10}$
$= -\frac{9}{5}$
或写作 $-1.8$
(3)
解:
$(-\frac{7}{3}) × (-1\frac{3}{14})$
$= (-\frac{7}{3}) × (-\frac{17}{14})$
$= \frac{119}{42}$
$= \frac{17}{6}$
或写作 $2\frac{5}{6}$
(4)
解:
$2.25 × (-\frac{8}{15})$
$= (\frac{9}{4}) × (-\frac{8}{15})$
$= -\frac{72}{60}$
$= -\frac{6}{5}$
或写作 $-1.2$
1. 已知$|a|= 3$,$|b|= 2$,且$ab<0$,则$a+b$的值等于(
A.5或-5
B.1或-1
C.5或1
D.-5或-1
B
)A.5或-5
B.1或-1
C.5或1
D.-5或-1
答案:
解:
∵|a|=3,|b|=2,
∴a=±3,b=±2,
∵ab<0,
∴a、b异号,
当a=3时,b=-2,则a+b=3+(-2)=1;
当a=-3时,b=2,则a+b=-3+2=-1,
综上,a+b的值为1或-1,
答案:B
∵|a|=3,|b|=2,
∴a=±3,b=±2,
∵ab<0,
∴a、b异号,
当a=3时,b=-2,则a+b=3+(-2)=1;
当a=-3时,b=2,则a+b=-3+2=-1,
综上,a+b的值为1或-1,
答案:B
2. 数$a$,$b$在数轴上的位置如图所示,下列式子正确的是(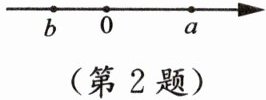
A.$a-b<0$
B.$a<b$
C.$ab<0$
D.$|a|<|b|$
C
)
A.$a-b<0$
B.$a<b$
C.$ab<0$
D.$|a|<|b|$
答案:
【解析】:
题目考查有理数在数轴上的位置关系及大小比较,以及有理数的乘法性质。
根据数轴图可知:
数 $a$ 在数轴右侧,为正数;数 $b$ 在数轴左侧,为负数,即 $a > 0$,$b < 0$。
分析选项:
A. $a - b < 0$:由于 $a$ 是正数,$b$ 是负数,正数减负数相当于加上一个正数,结果必定为正数,因此 $a - b > 0$,选项错误。
B. $a < b$:由于 $a$ 是正数,$b$ 是负数,正数必定大于负数,因此 $a > b$,选项错误。
C. $ab < 0$:由于 $a$ 是正数,$b$ 是负数,正数乘以负数结果必定为负数,因此 $ab < 0$,选项正确。
D. $|a| < |b|$:由于 $a$ 是正数,$b$ 是负数,且从数轴上看,$a$ 到原点的距离大于 $b$ 到原点的距离,因此 $|a| > |b|$,选项错误。
故正确答案为 C。
【答案】:C
题目考查有理数在数轴上的位置关系及大小比较,以及有理数的乘法性质。
根据数轴图可知:
数 $a$ 在数轴右侧,为正数;数 $b$ 在数轴左侧,为负数,即 $a > 0$,$b < 0$。
分析选项:
A. $a - b < 0$:由于 $a$ 是正数,$b$ 是负数,正数减负数相当于加上一个正数,结果必定为正数,因此 $a - b > 0$,选项错误。
B. $a < b$:由于 $a$ 是正数,$b$ 是负数,正数必定大于负数,因此 $a > b$,选项错误。
C. $ab < 0$:由于 $a$ 是正数,$b$ 是负数,正数乘以负数结果必定为负数,因此 $ab < 0$,选项正确。
D. $|a| < |b|$:由于 $a$ 是正数,$b$ 是负数,且从数轴上看,$a$ 到原点的距离大于 $b$ 到原点的距离,因此 $|a| > |b|$,选项错误。
故正确答案为 C。
【答案】:C
3. 直接填写计算得到的结果:
(1)$6×(-9)=$
(4)$4×(-\frac{3}{2})=$
(1)$6×(-9)=$
-54
; (2)$(-6)×(-9)=$54
; (3)$(-5)×0=$0
;(4)$4×(-\frac{3}{2})=$
-6
; (5)$(-8)×(-\frac{3}{2})=$12
.
答案:
【解析】:
题目考察的是有理数的乘法运算。根据有理数乘法的规则,正数乘以负数得负数,负数乘以负数得正数,任何数与0相乘都等于0。
(1) $6 × (-9)$ 的计算中,6是正数,-9是负数,所以结果是负数,具体为 $-54$。
(2) $(-6) × (-9)$ 的计算中,-6和-9都是负数,所以结果是正数,具体为 $54$。
(3) $(-5) × 0$ 的计算中,任何数与0相乘都等于0,所以结果是 $0$。
(4) $4 × (-\frac{3}{2})$ 的计算中,4是正数,$-\frac{3}{2}$ 是负数,所以结果是负数,将4乘到分子即得 $-6$。
(5) $(-8) × (-\frac{3}{2})$ 的计算中,-8和$-\frac{3}{2}$ 都是负数,所以结果是正数,将8乘到分子即得 $12$。
【答案】:
(1) $-54$
(2) $54$
(3) $0$
(4) $-6$
(5) $12$
题目考察的是有理数的乘法运算。根据有理数乘法的规则,正数乘以负数得负数,负数乘以负数得正数,任何数与0相乘都等于0。
(1) $6 × (-9)$ 的计算中,6是正数,-9是负数,所以结果是负数,具体为 $-54$。
(2) $(-6) × (-9)$ 的计算中,-6和-9都是负数,所以结果是正数,具体为 $54$。
(3) $(-5) × 0$ 的计算中,任何数与0相乘都等于0,所以结果是 $0$。
(4) $4 × (-\frac{3}{2})$ 的计算中,4是正数,$-\frac{3}{2}$ 是负数,所以结果是负数,将4乘到分子即得 $-6$。
(5) $(-8) × (-\frac{3}{2})$ 的计算中,-8和$-\frac{3}{2}$ 都是负数,所以结果是正数,将8乘到分子即得 $12$。
【答案】:
(1) $-54$
(2) $54$
(3) $0$
(4) $-6$
(5) $12$
查看更多完整答案,请扫码查看


