《2025年课课练江苏七年级数学上册苏科版》

例1 如图6.2.5,已知$\angle\alpha和\angle\beta$,请用直尺和圆规作图.
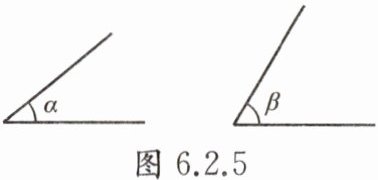
(1)作$\angle AOB$,使得$\angle AOB= \angle\alpha+\angle\beta$；
(2)作$\angle COD$,使得$\angle COD= \angle\beta-\angle\alpha$.

答案：
(1)解：①作射线OA；②以∠α的顶点为圆心，任意长为半径画弧，分别交∠α的两边于点M、N；③以O为圆心，同样长为半径画弧，交OA于点C；④以C为圆心，MN长为半径画弧，交前弧于点D，作射线OD，则∠AOD=∠α；⑤以∠β的顶点为圆心，任意长为半径画弧，分别交∠β的两边于点P、Q；⑥以D为圆心，PQ长为半径画弧，交∠AOD外侧的弧于点B，作射线OB，则∠AOB=∠α+∠β。
(2)解：①作射线OC；②以∠β的顶点为圆心，任意长为半径画弧，分别交∠β的两边于点E、F；③以O为圆心，同样长为半径画弧，交OC于点G；④以G为圆心，EF长为半径画弧，交前弧于点H，作射线OH，则∠COH=∠β；⑤以∠α的顶点为圆心，任意长为半径画弧，分别交∠α的两边于点I、J；⑥以H为圆心，IJ长为半径画弧，交∠COH内侧的弧于点D，作射线OD，则∠COD=∠β-∠α。

例2 如图6.2.6,$\angle AOD= 80^\circ$,射线$OC从\angle AOD的边OA$出发,绕点$O向边OD$旋转,$OB平分\angle AOC$,当$\angle BOC:\angle COD= 1:2$时,求$\angle AOB$的大小.

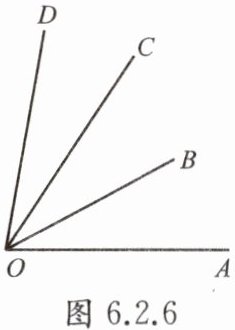
答案： 解：设∠AOB = x
∵OB平分∠AOC
∴∠BOC = ∠AOB = x
∵∠BOC : ∠COD = 1 : 2
∴∠COD = 2∠BOC = 2x
∵∠AOD = ∠AOB + ∠BOC + ∠COD = 80°
∴x + x + 2x = 80°
4x = 80°
x = 20°
即∠AOB = 20°

1. 射线$BD在\angle ABC$内部,下列式子中不能说明$BD是\angle ABC$的平分线的是 (B)
A.$\angle ABC= 2\angle ABD$
B.$\angle ABD+\angle CBD= \angle ABC$
C.$\angle CBD= \frac{1}{2}\angle ABC$
D.$\angle ABD= \angle CBD$

答案： 解：根据角平分线的定义，从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线。
选项A：若$\angle ABC = 2\angle ABD$，因为射线$BD$在$\angle ABC$内部，所以$\angle ABD=\angle CBD$，能说明$BD$是角平分线。
选项B：$\angle ABD+\angle CBD = \angle ABC$，这是角的和的定义，任何在$\angle ABC$内部的射线$BD$都满足此式，不能说明$BD$是角平分线。
选项C：若$\angle CBD=\frac{1}{2}\angle ABC$，则$\angle ABD=\angle ABC - \angle CBD=\frac{1}{2}\angle ABC$，所以$\angle ABD=\angle CBD$，能说明$BD$是角平分线。
选项D：$\angle ABD = \angle CBD$，直接符合角平分线定义，能说明$BD$是角平分线。
答案：B

2. 对于任意的$\angle\alpha和\angle\beta$,下列关于其大小关系的说法正确的是 (D)
A.$\angle\alpha＞\angle\beta$
B.不是$\angle\alpha＞\angle\beta$,就是$\angle\alpha＜\beta$
C.$\angle\alpha=\angle\beta$
D.$\angle\alpha＞\angle\beta$,$\angle\alpha=\angle\beta$,$\angle\alpha＜\angle\beta$这三种关系中必有一种正确

答案： 【解析】：
本题主要考察角的大小比较及角的基本性质。对于任意的两个角$\angle\alpha$和$\angle\beta$，它们之间的大小关系可以是大于、小于或等于。这三种关系是基于角度的数值来定义的。题目要求我们判断这三种关系中哪一种必然正确。
A选项表示$\angle\alpha＞\angle\beta$，这只是一种可能性，并不能保证对所有$\angle\alpha$和$\angle\beta$都成立。
B选项表示不是$\angle\alpha＞\angle\beta$，就是$\angle\alpha＜\angle\beta$，这忽略了$\angle\alpha$和$\angle\beta$可能相等的情况。
C选项表示$\angle\alpha=\angle\beta$，这同样只是一种可能性，并不能保证对所有$\angle\alpha$和$\angle\beta$都成立。
D选项表示$\angle\alpha＞\angle\beta$，$\angle\alpha=\angle\beta$，$\angle\alpha＜\angle\beta$这三种关系中必有一种正确，这符合角的基本性质，即任意两个角之间的大小关系必然是这三种之一。
【答案】：
D

3. 如图,$\angle AOB可以看成由OA绕点O$按逆时针方向旋转而成,$\angle AOC可以看成由OA绕点O$按逆时针方向旋转而成,则$\angle AOB与\angle AOC$的大小关系为$\angle AOB ＜ \angle AOC$.

答案： 【解析】：
本题考查角的大小比较。
根据题目描述，$\angle AOB$和$\angle AOC$都是由$OA$绕点$O$按逆时针方向旋转而成。
从图中可以看出，$\angle AOC$包含了$\angle AOB$和$\angle BOC$，即$\angle AOC = \angle AOB + \angle BOC$。
由于$\angle BOC$是一个正角（即角度大于$0^\circ$），
因此$\angle AOC$一定大于$\angle AOB$。
【答案】：$\angle AOB ＜ \angle AOC$。