《2025年零障碍导教导学案九年级物理全一册沪粤版》

2. 【古代科技】(2023·广东节选)明代宋应星在《天工开物》中记载的农业生产汲水装置——辘轳沿用至今。图甲是一种辘轳,由具有共同转动轴的大轮和小轮组成。提水时,用力使大轮转动,小轮随之转动并缠绕井绳,提起水桶。设大轮与小轮的半径比为3:1,水桶受到的总重力为90 N。使周长为3 m的大轮转动一圈,水桶匀速上升,井绳对水桶做功90J。(不计井绳的粗细和自重)

答案： 解：大轮周长为3m，转动一圈时，大轮边缘移动距离$s_{大}=3m$。
大轮与小轮半径比$r_{大}:r_{小}=3:1$，因共轴转动，大轮与小轮转动圈数相同，均为1圈。
小轮周长$C_{小}=2\pi r_{小}$，大轮周长$C_{大}=2\pi r_{大}=3m$，由$\frac{C_{大}}{C_{小}}=\frac{r_{大}}{r_{小}}=\frac{3}{1}$，得$C_{小}=\frac{C_{大}}{3}=1m$。
小轮转动一圈，井绳缠绕长度即水桶上升高度$h=C_{小}=1m$。
井绳对水桶做功$W=Gh=90N×1m=90J$。
答案：90

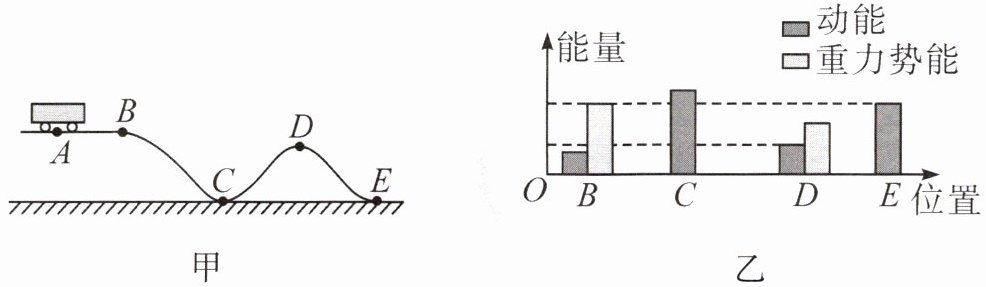
3. (2022·广东)图甲中过山车从A点出发,先后经过B、C、D、E点。图乙是过山车在B、C,D、E点的动能和重力势能大小的示意图,则过山车的动能在C点最大,B点重力势能的大小大于 (选填“大于”“等于”或“小于”)E点动能的大小。在这个过程中,过山车的机械能是变化 (选填“变化”或“不变”)的。

答案： 【解析】：
本题主要考查动能和重力势能的影响因素，以及机械能守恒的条件。
动能的大小与物体的质量和速度有关，质量越大、速度越大，动能就越大；重力势能的大小与物体的质量和高度有关，质量越大、高度越高，重力势能就越大。同时，还需要考虑机械能守恒的条件，即只有重力或弹力做功时，机械能才守恒，否则机械能会发生变化。
过山车从A点出发时，具有一定的重力势能，随着过山车的高度下降，重力势能逐渐转化为动能，速度逐渐增大。在C点，过山车的高度最低，速度最大，因此动能也最大。
从图乙中可以看出，B点的重力势能大小明显大于E点的动能大小。
在这个过程中，由于过山车需要克服摩擦力等因素做功，会消耗一部分机械能，因此过山车的机械能是变化的。
【答案】：
C；大于；变化

4. 【航空航天】(2024·广东节选)2024年4月30日,神舟十七号载人飞船返回舱成功着陆,如图所示。若返回舱质量为$3× 10^{3}\ kg$,在着陆过程中,从距地面1 m高处竖直向下落地,用时0.4 s。g取10 N/kg,求返回舱在这段时间内：(1)返回舱的平均速度。(2)返回舱重力做的功。

答案： 【解析】：
本题主要考查速度公式和功的计算公式的应用。
（1）要求返回舱的平均速度，我们可以使用速度公式$v = \frac{s}{t}$，其中s是路程，t是时间。
（2）要求返回舱重力做的功，我们可以使用功的计算公式$W = Fs$，其中F是力，s是在力的方向上移动的距离。在本题中，力F就是返回舱的重力$G=mg$。
【答案】：
(1)解：由题知，返回舱从距地面$1m$高处竖直向下落地，用时$0.4s$，
所以返回舱在这段时间内的平均速度为：
$v = \frac{s}{t} = \frac{1 m}{0.4 s} = 2.5 m/s$；
答：返回舱的平均速度为$2.5m/s$；
(2)解：已知返回舱质量$m=3 × 10^{3} kg$，$g$取$10N/kg$，
所以返回舱的重力为：$G = mg = 3 × 10^{3} kg × 10 N/kg = 3 × 10^{4} N$，
重力做的功为：$W = Gh = 3 × 10^{4} N × 1 m = 3 × 10^{4} J$。
答：返回舱重力做的功为$3 × 10^{4}J$。