《2025年零障碍导教导学案九年级物理全一册沪粤版》

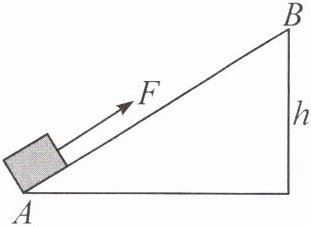
例3 如图所示,斜面长$s= 10\ m$,高$h= 4\ m$,用沿斜面方向的推力F,将一个重为100 N的物体由斜面底端A匀速推到顶端B。运动过程中物体克服摩擦力做了100 J的功。求：
(1)运动过程中克服物体的重力做的功。
(2)斜面的机械效率。
(3)摩擦力的大小。

答案： 【解析】：
本题主要考查了功的计算、机械效率的计算以及二力平衡条件的应用，要知道物体沿斜面上升时，用沿斜面方向的推力$F$做的功为总功，克服重力做的功为有用功，克服摩擦力做的功为额外功，且总功等于有用功与额外功之和。
（1）知道物体的重力和斜面的高度，根据$W = Gh$求出克服物体的重力做的功，即有用功。
（2）知道运动过程中物体克服摩擦力做的功，即额外功，又知道有用功，根据$W_{总} = W_{有} + W_{额}$求出总功，再根据$\eta = \frac{W_{有}}{W_{总}} × 100\%$求出斜面的机械效率。
（3）知道斜面的长度和额外功，根据$W_{额} = fs$求出摩擦力的大小。
【答案】：
(1)运动过程中克服物体的重力做的功：$W_{有} = Gh = 100× 4 = 400J$。
答：运动过程中克服物体的重力做的功为$400J$。
(2)运动过程做的总功：$W_{总} = W_{有} + W_{额} = 400 + 100 = 500J$，
斜面的机械效率$\eta = \frac{W_{有}}{W_{总}} × 100\% = \frac{400}{500} × 100\% = 80\%$。
答：斜面的机械效率为$80\%$。
(3)由$W_{额} = fs$得，摩擦力的大小：$f = \frac{W_{额}}{s} = \frac{100}{10} = 10N$。
答：摩擦力的大小为$10N$。

练习3 如图所示是为了上山方便而修建的盘山公路,我们把盘山公路简化为一个斜面模型。一辆重$6.3×10^{4}\ N$的小型货车从山脚匀速行驶到竖直高度为500 m的山顶,货车通过的路程为3600 m。已知从山脚开上山顶,货车所受牵引力和摩擦力保持不变,且牵引力大小为$2.5×10^{4}\ N$,则货车从山脚开到山顶的过程中,求：
(1)牵引力所做的功。
(2)该盘山公路的机械效率。
(3)行驶过程中货车所受摩擦力。

答案： 【解析】：
本题主要考查了功的计算、机械效率的计算以及二力平衡条件的应用。
（1）知道牵引力和在牵引力方向上移动的距离，根据$W = Fs$求出牵引力做的功，即总功。
（2）知道货车的重力和上升的高度，根据$W = Gh$求出有用功，利用效率公式求出斜面的机械效率。
（3）根据$W_{总} = W_{有} + W_{额}$求出额外功，额外功为克服摩擦力做的功，再根据$W_{额} = fs$求出摩擦力的大小。
【答案】：
解：（1）牵引力做的功：
$W_{总} = Fs = 2.5 × 10^{4} × 3600 = 9 × 10^{7}J$；
（2）货车做的有用功：
$W_{有} = Gh = 6.3 × 10^{4} × 500 = 3.15 × 10^{7}J$，
盘山公路的机械效率：
$\eta = \frac{W_{有}}{W_{总}} × 100\% = \frac{3.15 × 10^{7}}{9 × 10^{7}} × 100\% = 35\%$；
（3）货车做的额外功：
$W_{额} = W_{总} - W_{有} = 9 × 10^{7} - 3.15 × 10^{7} = 5.85 × 10^{7}J$，
由$W_{额} = fs$得，货车所受摩擦力：
$f = \frac{W_{额}}{s} = \frac{5.85 × 10^{7}}{3600} = 1.625 × 10^{4}N$。
答：（1）牵引力所做的功为$9 × 10^{7}J$；
（2）该盘山公路的机械效率为$35\%$；
（3）行驶过程中货车所受摩擦力为$1.625 × 10^{4}N$。

1. 无人机应用广泛,现在无人机的很多钢材部件用密度更小的碳纤维替换,来减轻机身重量。如图所示,用碳纤维替换后的无人机与未替换前的相比,将同一个快递包裹从地面运送到五楼,可以(C)

A.减小有用功
B.增大有用功
C.减小额外功
D.增大额外功

答案： 【解析】：
本题可根据有用功和额外功的概念，结合题目中无人机钢材部件用碳纤维替换这一条件，分析无人机将同一个快递包裹从地面运送到五楼时有用功和额外功的变化情况。
有用功：有用功是指对人们有用的功，在本题中，将快递包裹从地面运送到五楼，克服快递包裹重力所做的功就是有用功。根据公式$W_{有}=Gh$（其中$G$是快递包裹的重力，$h$是上升的高度），因为快递包裹不变，即$G$不变，上升的高度$h$也不变，所以有用功不变。
额外功：额外功是指并非我们需要但又不得不做的功，本题中无人机自身的重力产生的功是额外功。用碳纤维替换钢材部件后，无人机的质量减小，根据$G = mg$（其中$m$是质量，$g$是重力加速度）可知，无人机的重力减小。在上升高度$h$不变的情况下，根据$W_{额}=G_{机}h$（其中$G_{机}$是无人机的重力），可得额外功减小。
【答案】：
C