《2025年零障碍导教导学案九年级物理全一册沪粤版》

3.如图所示的四个电路中,电源电压U相同,$R_{1}\lt R_{2}$,相同时间内整个电路产生的总热量由大到小的顺序是(B)

A.甲、乙、丙、丁
B.丁、甲、乙、丙
C.丁、丙、乙、甲
D.丙、乙、甲、丁

答案： 【解析】：
首先我们知道电路中产生的总热量等于电路中电流做的功, 即 $Q = W = \frac{U^2}{R}t$，且电源电压 $U$ 和时间 $t$ 相同，因此总热量 $Q$ 与总电阻 $R$ 成反比。
分析各电路的总电阻：
甲图中只有电阻 $R_1$，
乙图中只有电阻 $R_2$，
丙图中 $R_1$ 和 $R_2$ 串联，总电阻为 $R_1 + R_2$，
丁图中 $R_1$ 和 $R_2$ 并联，总电阻为 $\frac{R_1R_2}{R_1 + R_2}$。
已知 $R_1 ＜ R_2$，因此：
串联时总电阻最大，即丙图的总电阻最大，
并联时总电阻最小，即丁图的总电阻最小，
单独 $R_1$ 时电阻较小，即甲图的总电阻较小，
单独 $R_2$ 时电阻较大，即乙图的总电阻较大。
根据总电阻的大小，可以得出总热量的大小顺序为：丁 ＞ 甲 ＞ 乙 ＞ 丙。
【答案】： B.丁、甲、乙、丙

4.通过110 Ω电阻丝的电流是2 A,产生4400 J的热量所用时间为10s,电阻丝两端的电压是220V。

答案： 解：
由焦耳定律$Q = I^{2}Rt$得，产生$4400J$热量所用时间：
$t=\frac{Q}{I^{2}R}=\frac{4400J}{(2A)^{2}×110\Omega}=\frac{4400J}{4A^{2}×110\Omega}=\frac{4400J}{440A^{2}\cdot\Omega}=10s$
由欧姆定律$I=\frac{U}{R}$得，电阻丝两端的电压：
$U = IR=2A×110\Omega = 220V$
10；220

5.如图甲、乙、丙所示是“探究电流通过导体产生热量的多少跟什么因素有关”实验的部分装置。

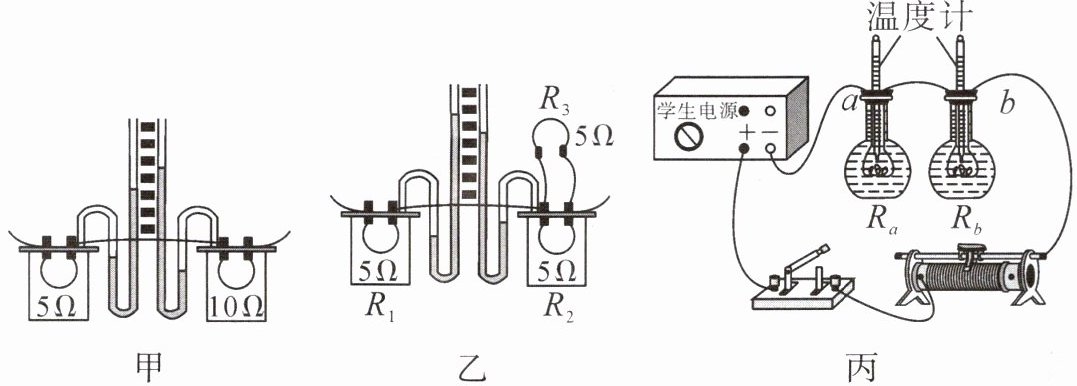
(1)实验中,通过观察U形管左右两侧液面的高度差来比较电流通过导体产生热量的多少。
(2)将图甲装置接入电路中,是为了探究电流通过导体产生热量的多少与电流的关系。
(3)图乙装置中将$R_{3}与R_{2}$并联是为了控制电阻丝$R_{1}和R_{2}$的电流大小不同。
(4)利用图丙装置探究液体吸热能力的大小时,在a、b两瓶内装入质量、初温都相同的不同液体,且$R_{a}= R_{b}$。通电一段时间后,观察到b瓶内液体温度高一些,可判断b瓶内液体的吸热能力较弱(选填“强”或“弱”)。

答案： 【解析】：
（1）实验中根据U形管内液面的高度差来判断电流产生热量的多少，采用了转换法。
（2）图甲装置中一个$5\Omega$的电阻与两个$5\Omega$的电阻并联后再串联，根据串联电路的电流特点可知，右端两个电阻的总电流和左端的电阻电流相等，即$I_右=I_左$，两个$5\Omega$的电阻并联，根据并联电路的电流特点知$I_左=I_1+I_2$，两电阻阻值相等，则支路中电流相等，$I_1=I_2$，所以右边容器中的通过电阻的电流是左侧通过电流的一半，即$I_左=2I_右$，所以该装置是研究电流产生的热量与电流的关系。
（3）图乙装置中将$R_{3}$与$R_{2}$并联，根据并联电路的电流特点，$I_1=I_2+I_3$，为了控制电阻丝$R_{1}$和$R_{2}$的电流大小不同；
（4）在a、b两瓶内装入质量、初温都相同的不同液体，两电阻丝的阻值$R_{a}= R_{b}$，通电一段时间后，观察到b瓶内液体温度高一些，根据$Q=cm\Delta t$，在质量，吸收的热量相同的情况下，温度变化量越大，比热容越小，吸热能力越弱，故可判断b瓶内液体的吸热能力较弱。
【答案】：
(1)高度差
(2)电流
(3)电流
(4)弱

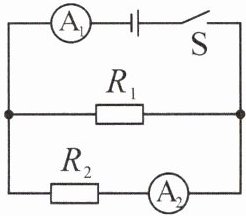
6.如图所示,电源两端电压保持不变,电阻$R_{1}$阻值为20 Ω,闭合开关S后,电流表$A_{1}$的示数为0.5 A,电流表$A_{2}$的示数为0.2 A。求：
(1)电源电压U。
(2)电阻$R_{2}$的阻值。
(3)5 min内电流通过$R_{1}$产生的热量。

答案： 解：
(1)由图知，R₁与R₂并联，电流表A₁测干路电流，A₂测R₂支路电流。
通过R₁的电流I₁=I - I₂=0.5A - 0.2A=0.3A
电源电压U=U₁=I₁R₁=0.3A×20Ω=6V
(2)电阻R₂的阻值R₂=U/I₂=6V/0.2A=30Ω
(3)t=5min=300s
电流通过R₁产生的热量Q₁=I₁²R₁t=(0.3A)²×20Ω×300s=540J
答：
(1)电源电压U为6V；
(2)电阻R₂的阻值为30Ω；
(3)5min内电流通过R₁产生的热量为540J。