《2025年名校题库八年级数学上册北师大版》

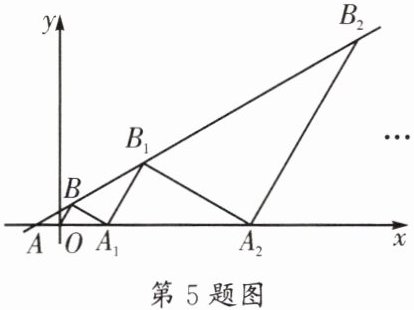
5. (金牛区期末)如图,在平面直角坐标系$xOy$中,射线$AO与x$轴重合,已知$∠BAO= 30^{\circ }$,$OA= OB= 1$,过点$B作BA_{1}⊥OB交x轴于点A_{1}$,过点$A_{1}作B_{1}A_{1}⊥BA_{1}交直线AB于点B_{1}$,过点$B_{1}作B_{1}A_{2}⊥B_{1}A_{1}交x轴于点A_{2}$,过点$A_{2}作A_{2}B_{2}⊥B_{1}A_{2}交直线AB于点B_{2}$,重复操作,依次得到点$B_{3},B_{4},...,B_{n}$,则点$B$的坐标为______,点$B_{n}$的坐标为______(用含$n$的式子表示). (提示:含$30^{\circ }$角的直角三角形,三边之比为$1:\sqrt {3}:2$)

答案：
($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)　($\frac{3^{n + 1}}{2}$−1,$\frac{(\sqrt{3})^{2n + 1}}{2}$)　[解析]
∵OB =OA=1,
∴∠BAO=∠ABO=30°,
∴∠BOA1=60°.
∵∠A1BO=90°,
∴∠BA1O=30°,
∴BA1=$\sqrt{3}$.同理可得∠BB1A1=30°,
∴B1A1=($\sqrt{3}$)².同理可得B1A2=($\sqrt{3}$)³,A2B2=($\sqrt{3}$)⁴,…,AnBn=($\sqrt{3}$)²ⁿ.如图,过点B作BC⊥OA1于点C,则∠OBC=30°,OB=1,
∴BC=$\frac{\sqrt{3}}{2}$,OC=$\frac{1}{2}$，
∴B ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).过点Bn作BnD⊥OAₙ₊₁于点D,则∠AnBnD=30°,
∴BnD=$\frac{\sqrt{3}}{2}$×($\sqrt{3}$)²ⁿ=$\frac{(\sqrt{3})^{2n + 1}}{2}$,
∴AD=$\sqrt{3}$×$\frac{(\sqrt{3})^{2n + 1}}{2}$=$\frac{3^{n + 1}}{2}$,
∴OD=AD−OA=$\frac{3^{n + 1}}{2}$−1,
∴Bn($\frac{3^{n + 1}}{2}$−1,$\frac{(\sqrt{3})^{2n + 1}}{2}$).

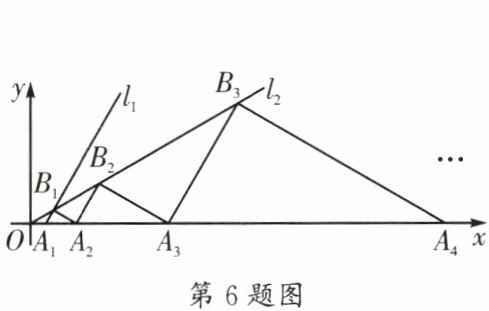
6. (成华区期末)如图,直线$l_{1}:y= \sqrt {3}x-\sqrt {3}与x轴交于点A_{1}$,与直线$l_{2}:y= \frac {\sqrt {3}}{3}x交于点B_{1}$,过点$B_{1}作l_{1}的垂线交x轴于点A_{2}$,过点$A_{2}作l_{1}的平行线交l_{2}于点B_{2}$,过点$B_{2}作l_{1}的垂线交x轴于点A_{3}$,过点$A_{3}作l_{1}的平行线交l_{2}于点B_{3}$……按此规律作下去,则点$B_{2024}$的坐标是______.

答案：
($\frac{3^{2024}}{2}$,$\frac{3^{2023}}{2}\sqrt{3}$)　[解析]如图,分别过点B1,B2,B3作x轴的垂线，垂足分别为C1,C2,C3.
∵直线l1:y=$\sqrt{3}$x−$\sqrt{3}$与x轴的夹角为60°,点A1的坐标为(1,0),
∴OA1=1,∠B1A1A2=60°.
∵直线l2:y=$\frac{\sqrt{3}}{3}$x经过坐标原点，且与x轴的夹角为30°,
∴∠B1OA1=30°.
∵∠B1A1A2=∠B1OA1+∠OB1A1,
∴60°=30°+∠OB1A1,
∴∠OB1A1=30°,
∴OA1=A1B1=1.
∵A2B1⊥直线l1,
∴∠A2B1A1=90°,
∴∠A1A2B1=30°,
∴A1A2=2A1B1=2.在Rt△A1A2B1中,A1A2=2,A1B1=1,由勾股定理得A2B1=$\sqrt{A1A2²−A1B1²}$=$\sqrt{3}$,由三角形的面积公式得△A1A2B1的面积=$\frac{1}{2}$A1A2·B1C1=$\frac{1}{2}$A1B1·A2B1,
∴B1C1=$\frac{A1B1·A2B1}{A1A2}$=$\frac{1×\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.在Rt△A1B1C1中,A1B1=1,B1C1=$\frac{\sqrt{3}}{2}$,由勾股定理得A1C1=$\sqrt{A1B1²−B1C1²}$=$\frac{1}{2}$,
∴OC1=OA1+A1C1=1+$\frac{1}{2}$=$\frac{3}{2}$,
∴点B1的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
∵A2B1⊥直线l1,A2B2//直线l1,
∴A2B1⊥A2B2,∠A2B2B1=∠OB1A1=30°,∠B2A2A3=∠B1A1A2=60°,
∴B1B2=2A2B1=2$\sqrt{3}$.由勾股定理得A2B2=$\sqrt{B1B2²−A2B1²}$=3.
∵A3B2⊥直线l1,
∴在Rt△A2A3B2中,∠B2A2A3=60°,
∴∠A2A3B2=30°,
∴A2A3=2A2B2=6.由勾股定理得A3B2=$\sqrt{A2A3²−A2B2²}$=3$\sqrt{3}$,由三角形的面积公式得△A2A3B2的面积=$\frac{1}{2}$A2A3·B2C2=$\frac{1}{2}$A2B2·A3B2,
∴B2C2=$\frac{A2B2·A3B2}{A2A3}$=$\frac{3\sqrt{3}}{2}$,在Rt△A2C2B2中,A2B2=3,B2C2=$\frac{3\sqrt{3}}{2}$,由勾股定理得A2C2=$\sqrt{A2B2²−B2C2²}$=$\frac{3}{2}$,
∴OC2=OA1+A1A2+A2C2=1+2+$\frac{3}{2}$=$\frac{9}{2}$,
∴点B2的坐标为($\frac{9}{2}$,$\frac{3\sqrt{3}}{2}$).同理可得:点B3的坐标为($\frac{27}{2}$,$\frac{9\sqrt{3}}{2}$),点B4的坐标为($\frac{81}{2}$,$\frac{27\sqrt{3}}{2}$),……,以此类推,点Bn的坐标为($\frac{3^n}{2}$,$\frac{3^{n - 1}}{2}\sqrt{3}$),
∴当n=2024时,$\frac{3^n}{2}$=$\frac{3^{2024}}{2}$,$\frac{3^{n - 1}}{2}\sqrt{3}$=$\frac{3^{2023}}{2}\sqrt{3}$,
∴点B2024的坐标为($\frac{3^{2024}}{2}$,$\frac{3^{2023}}{2}\sqrt{3}$).

1. (嘉祥)如图,已知直线$y= -\frac {1}{2}x+2与坐标轴交于点B$,$A$。过线段$AB的中点A_{1}作A_{1}B_{1}⊥x轴于点B_{1}$,过线段$A_{1}B的中点A_{2}作A_{2}B_{2}⊥x轴于点B_{2}$,过线段$A_{2}B的中点A_{3}作A_{3}B_{3}⊥x轴于点B_{3}$……以此类推,则$\triangle A_{2022}B_{2022}B_{2021}$的面积为______$\frac{1}{2^{4042}}$。

答案： 解：对于直线$y=-\frac{1}{2}x + 2$，
- 当$x=0$时，$y=2$，得$A(0,2)$；当$y=0$时，$-\frac{1}{2}x + 2=0$，解得$x=4$，得$B(4,0)$。
$AB$中点$A_1$坐标为$(\frac{0 + 4}{2},\frac{2 + 0}{2})=(2,1)$，$A_1B_1\perp x$轴于$B_1$，则$B_1(2,0)$。
$A_1B$中点$A_2$坐标为$(\frac{2 + 4}{2},\frac{1 + 0}{2})=(3,\frac{1}{2})$，$A_2B_2\perp x$轴于$B_2$，则$B_2(3,0)$，$B_1B_2=3 - 2=1$，$A_2B_2=\frac{1}{2}$，$S_{\triangle A_2B_2B_2021}=\frac{1}{2}×1×\frac{1}{2}=\frac{1}{4}=\frac{1}{4^1}$。
$A_2B$中点$A_3$坐标为$(\frac{3 + 4}{2},\frac{\frac{1}{2}+ 0}{2})=(\frac{7}{2},\frac{1}{4})$，$A_3B_3\perp x$轴于$B_3$，则$B_3(\frac{7}{2},0)$，$B_2B_3=\frac{7}{2}-3=\frac{1}{2}$，$A_3B_3=\frac{1}{4}$，$S_{\triangle A_3B_3B_2}=\frac{1}{2}×\frac{1}{2}×\frac{1}{4}=\frac{1}{16}=\frac{1}{4^2}$。
同理可得：$S_{\triangle A_nB_nB_{n - 1}}=\frac{1}{4^{n - 1}}$。
当$n = 2022$时，$S_{\triangle A_{2022}B_{2022}B_{2021}}=\frac{1}{4^{2021}}=\frac{1}{2^{4042}}$。
答案：$\frac{1}{2^{4042}}$

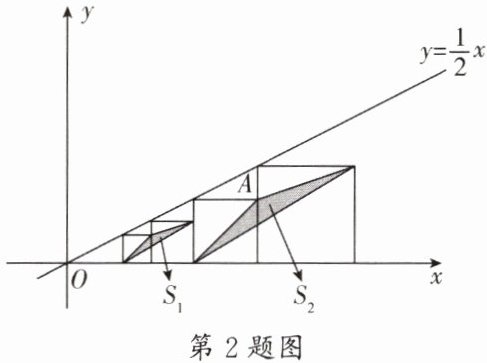
2. (高新区期末)如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数$y= \frac {1}{2}x$的图象上,从左向右第$3个正方形中的一个顶点A的坐标为(12,4)$,阴影三角形部分的面积从左向右依次记为$S_{1}$,$S_{2}$,$S_{3}$,…,$S_{n}$,则第$4$个正方形的边长是______,$S_{3}$的值为______。

6$\frac{81}{2}$

答案： 解：
$\because$ 点 $A(12,4)$ 在第 $3$ 个正方形中，且函数 $y=\frac{1}{2}x$ 的图象过该顶点，
$\therefore$ 第 $4$ 个正方形的边长为 $\frac{1}{2} × 12 = 6$。
由直线 $y=\frac{1}{2}x$ 性质，后一个正方形边长是前一个的 $\frac{3}{2}$ 倍，
$\therefore$ 第 $5$ 个正方形边长：$6 × \frac{3}{2} = 9$，
第 $6$ 个正方形边长：$9 × \frac{3}{2} = \frac{27}{2}$。
$S_3 = \frac{1}{2} × 9^2 + \frac{1}{2} × (9 + \frac{27}{2}) × \frac{27}{2} - \frac{1}{2} × (9 + \frac{27}{2}) × \frac{27}{2} = \frac{81}{2}$。
第 $4$ 个正方形的边长是 $6$，$S_3$ 的值为 $\frac{81}{2}$。
答案：$6$；$\frac{81}{2}$