《2025年名校题库八年级数学上册北师大版》

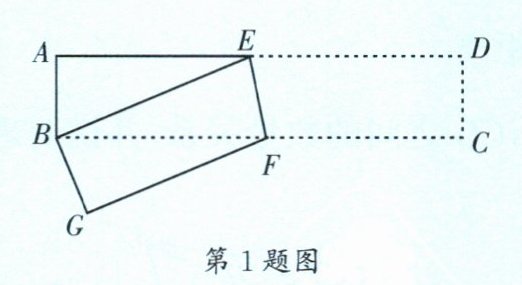
1. (锦江区期末)如图,在长方形ABCD中,AB= 5,AD= 25,将此长方形折叠,使点D与点B重合,折痕为EF,则BE的长为 (D)

A.12
B.8
C.10
D.13

答案： 解：设BE的长为x。
由折叠性质知，BE=DE=x。
因为AD=25，所以AE=AD-DE=25-x。
在长方形ABCD中，∠A=90°，AB=5。
在Rt△ABE中，根据勾股定理得：AB²+AE²=BE²，即5²+(25-x)²=x²。
展开得：25+625-50x+x²=x²。
化简得：650-50x=0，解得x=13。
答案：D

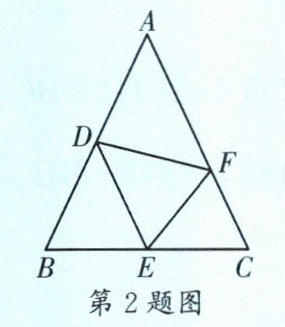
2. (西川)如图,在△ABC中,AB= AC,∠A＜90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,且点B和点F关于直线DE对称。若AD= DF,AB= 5,BC= 4,则CF= ______。

答案：
$\frac{8}{5}$　[解析]如图,连接 BF.
∵ 点 B 和点 F 关于直线 DE 对称,$\therefore BD=DF,\therefore ∠DBF=∠DFB.$$\because AD=DF,\therefore ∠A=∠DFA.\because ∠A+∠DFA+∠DFB+∠DBF=180^{\circ },\therefore 2∠DFA+2∠DFB=180^{\circ },\therefore ∠DFA+∠DFB=90^{\circ }$,即$∠AFB=90^{\circ },\therefore ∠BFC=90^{\circ }.\because AB=AC=5,BC=4$,由勾股定理,得$AB^{2}-AF^{2}=BC^{2}-CF^{2}=BF^{2},\therefore 5^{2}-(5 - CF)^{2}=4^{2}-CF^{2},\therefore CF=\frac{8}{5}$.

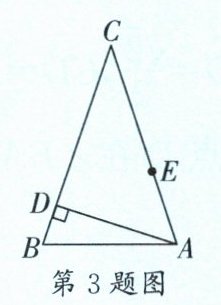
3. (武侯区期末)如图,在△ABC中,CA= CB= 10,AD⊥BC于点D,且AD:CD= 3:4,折叠△ABC使点C与点B重合,折痕交AC于点E,则线段AE的长为______。

答案：
$\frac{15}{4}$　[解析]设$AD = 3a,CD = 4a$.在$Rt△ACD$中,由勾股定理,得$AC = \sqrt{AD^{2}+CD^{2}} = 5a$.$\because CA = CB = 10 = 5a,\therefore a = 2,\therefore AD = 6,CD = 8$.如图,过点 B 作$BG⊥AC$于点 G,连接 BE.在$△ACD$和$△BCG$中,$\begin{cases} ∠ADC = ∠BGC \\ ∠C = ∠C \\ CA = CB \end{cases}$,$\therefore △ACD≌△BCG(AAS),\therefore CD = CG = 8,AD = BG = 6$.
∵ 折叠后,点 C 与点 B 重合,$\therefore CE = BE$.设$CE = BE = x$,则$EG = CG - CE = 8 - x,AE = AC - CE = 10 - x$.在$Rt△BEG$中,$BG^{2}+EG^{2}=BE^{2},\therefore 6^{2}+(8 - x)^{2}=x^{2}$,解得$x = \frac{25}{4}$,$\therefore AE = 10 - x = 10 - \frac{25}{4} = \frac{15}{4}$.

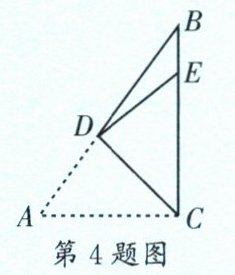
4. (武侯区期末)如图,在Rt△ACB中,∠ACB= 90°,点D在边AB上,连接CD,将△ADC沿直线CD翻折,点A恰好落在BC边上的点E处,若AC= 3,BE= 1,则DE的长是______。

答案：
$\frac{15}{7}$　[解析]如图,过点 D 作$DH⊥AC$于点 H,作$DF⊥BC$于点 F.
∵ 将$△ADC$沿直线 CD 翻折,$\therefore CE = AC = 3,∠BCD = ∠ACD = 45^{\circ },\therefore BC = 4$.$\because DH⊥AC,DF⊥BC,∠ACD = ∠BCD = 45^{\circ },\therefore DF = DH,∠FDC = ∠DCF = 45^{\circ },\therefore DF = CF$.$\because AB^{2}=AC^{2}+BC^{2}=9 + 16 = 25,\therefore AB = 5$.$\because S_{△ABC}=\frac{1}{2}×AC×BC=\frac{1}{2}×AC×DH+\frac{1}{2}×BC×DF,\therefore 6 = \frac{7}{2}DF,\therefore DF = \frac{12}{7},\therefore CF = DF = \frac{12}{7}$,$\therefore EF = CE - CF = 3 - \frac{12}{7} = \frac{9}{7}$,$\therefore DE = \sqrt{DF^{2}+EF^{2}}=\sqrt{\frac{144}{49}+\frac{81}{49}}=\frac{15}{7}$.

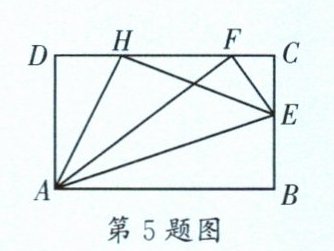
5. (七初)如图,在长方形ABCD中,AB= 5,AD= 3,E是BC边上一点,沿AE将△ABE折叠,点B的对应点正好落在CD边上的点F处,再作∠DAF的平分线交CD边于点H,连接EH,则△EFH的面积是______。

答案：
$\frac{5}{3}$　[解析]如图,过点 H 作$HG⊥AF$于点 G,则$∠FGH = ∠AGH = 90^{\circ }$.在长方形 ABCD 中,$∠D = 90^{\circ },CD = AB = 5,BC = AD = 3$.由折叠,得$AF = AB = 5,FE = BE,\therefore DF = \sqrt{AF^{2}-AD^{2}}=\sqrt{5^{2}-3^{2}} = 4$.$\because ∠AGH = ∠D = 90^{\circ },∠GAH = ∠DAH,AH = AH,\therefore △AGH≌△ADH(AAS),\therefore AG = AD = 3,GH = DH,\therefore FG = AF - AG = 5 - 3 = 2,GH = DH = DF - FH = 4 - FH$.$\because GH^{2}+FG^{2}=FH^{2},\therefore (4 - FH)^{2}+2^{2}=FH^{2}$,解得$FH = \frac{5}{2}$.$\because ∠C = 90^{\circ },\therefore CE^{2}+CF^{2}=FE^{2}$.$\because CF = CD - DF = 5 - 4 = 1,FE = BE = BC - CE = 3 - CE,\therefore CE^{2}+1^{2}=(3 - CE)^{2}$,解得$CE = \frac{4}{3}$.$\because CE⊥FH,\therefore S_{△EFH}=\frac{1}{2}FH\cdot CE=\frac{1}{2}×\frac{5}{2}×\frac{4}{3}=\frac{5}{3}$.

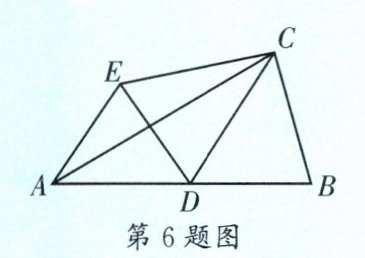
6. (金牛区期末)如图,在△ABC中,CD是中线,作点B关于CD对称的点为点E,连接CE,DE,AE,若AE= 1/2AB= 1,BC= √13/4,则点D到EC的距离为______。

答案：
$\frac{3\sqrt{39}}{26}$　[解析]如图,连接 BE,交 CD 于点 O,过点 D 作$DF⊥CE$于点 F.
∵ 点 B 关于 CD 对称的点为点 E,$\therefore CD⊥BE,OB = OE = \frac{1}{2}BE,\therefore EC = BC = \frac{\sqrt{13}}{4}$.$\because CD$为$△ABC$的中线,$\therefore AD = BD = \frac{1}{2}AB = 1,\therefore OD$为$△ABE$的中位线,$\therefore AE// CD,\therefore AE⊥BE,\therefore DE = \frac{1}{2}AB = 1$.在$Rt△ABE$中,$AE = 1,AB = 2$,由勾股定理,得$BE = \sqrt{AB^{2}-AE^{2}}=\sqrt{2^{2}-1^{2}} = \sqrt{3},\therefore OE = \frac{1}{2}BE = \frac{\sqrt{3}}{2}$.在$Rt△DOE$中,由勾股定理,得$OD = \sqrt{DE^{2}-OE^{2}}=\sqrt{1^{2}-(\frac{\sqrt{3}}{2})^{2}} = \frac{1}{2}$.在$Rt△COE$中,由勾股定理,得$OC = \sqrt{EC^{2}-OE^{2}}=\sqrt{(\frac{\sqrt{13}}{4})^{2}-(\frac{\sqrt{3}}{2})^{2}} = \frac{1}{4},\therefore CD = OD + OC = \frac{1}{2}+\frac{1}{4}=\frac{3}{4}$.$\because S_{△CDE}=\frac{1}{2}CD\cdot OE=\frac{1}{2}CE\cdot DF,\therefore DF = \frac{CD\cdot OE}{CE}=\frac{\frac{3}{4}×\frac{\sqrt{3}}{2}}{\frac{\sqrt{13}}{4}}=\frac{3\sqrt{39}}{26}$,即点 D 到 EC 的距离为$\frac{3\sqrt{39}}{26}$.

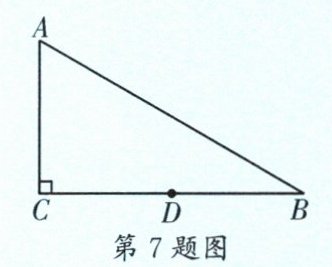
7. (石室天府)如图,在Rt△ABC中,∠C= 90°,∠B= 30°,BC= 4,D是BC的中点,E是边AB上一动点,沿DE所在直线把△BDE翻折得到△B'DE,直线B'D交AB于点F,如果△AB'F为直角三角形,那么BE的长为______。

答案：
$\frac{2\sqrt{3}}{3}$或$\frac{4\sqrt{3}}{5}$　[解析]①如图 1,当$∠AFB' = 90^{\circ }$时,在$Rt△ABC$中,$∠B = 30^{\circ },BC = 4$,设$AC = m$,则$AB = 2m,AB^{2}=BC^{2}+AC^{2},\therefore (2m)^{2}=4^{2}+m^{2}$,解得$m = \frac{4\sqrt{3}}{3}$(负值已舍去),则$AB = \frac{8}{3}\sqrt{3}$.$\because D$是 BC 的中点,$\therefore BD = CD = \frac{1}{2}BC = 2$.$\because ∠AFB' = ∠BFD = 90^{\circ },∠ACB = 90^{\circ },\therefore \frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot DF×2,\therefore DF = 1$.$\because ∠B = 30^{\circ },\therefore BF = \sqrt{3}$.过点 E 作$EH⊥BD$于点 H. 由折叠知$S_{△DB'E}=S_{△DBE},BD = B'D,\therefore \frac{1}{2}B'D\cdot EF=\frac{1}{2}BD\cdot EH,\therefore EF = EH$.$\because ∠B = 30^{\circ },\therefore \frac{BE}{EH}=\frac{\sqrt{3}-EH}{EH}=2$,解得$EH = \frac{\sqrt{3}}{3},\therefore BE = \frac{2\sqrt{3}}{3}$.

②如图 2,当$∠AB'F = 90^{\circ }$时,连接 AD,过点 E 作$EH⊥AB'$,交$AB'$的延长线于点 H.$\because ∠C = ∠AB'D = 90^{\circ },AD = AD,CD = DB = DB',\therefore Rt△ADC≌Rt△ADB'(HL),\therefore AC = AB' = \frac{4\sqrt{3}}{3}$.由折叠知$∠B = ∠DB'E,BE = B'E$.$\because AB'⊥DB',EH⊥AH,\therefore DB'// EH,\therefore ∠DB'E = ∠B'EH,\therefore ∠B = ∠B'EH = 30^{\circ }$.设$BE = x$,则$B'H = \frac{1}{2}x,EH = \frac{\sqrt{3}}{2}x$.在$Rt△AEH$中,$AH^{2}+EH^{2}=AE^{2},\therefore (\frac{1}{2}x+\frac{4\sqrt{3}}{3})^{2}+(\frac{\sqrt{3}}{2}x)^{2}=(\frac{8\sqrt{3}}{3}-x)^{2}$,解得$x = \frac{4\sqrt{3}}{5}$,则$BE = \frac{4\sqrt{3}}{5}$.故 BE 的长为$\frac{2\sqrt{3}}{3}$或$\frac{4\sqrt{3}}{5}$.

8. (树德实验)如图1,在矩形ABCD中,AB= 8,BC= 10,P是边AD上一点,将△ABP沿着直线BP翻折得到△A'BP。当AP= 8时,A'D= ______。如图2,连接A'C,当AP= 2时,此时△A'BC的面积为______。

答案：
$2\sqrt{17}$　$\frac{600}{17}$　[解析]如图 1,当$AP = 8$时,由折叠,知$AB = A'B,AP = A'P,∠APB = ∠A'PB,∠ABP = ∠A'BP,∠A = ∠BA'P = 90^{\circ },\therefore $四边形$ABA'P$是正方形,$\therefore A'P = 8,PD = 2,\therefore A'D = \sqrt{A'P^{2}+PD^{2}}=\sqrt{8^{2}+2^{2}} = 2\sqrt{17}$

如图 2,当$AP = 2$时,过点$A'$作$MN// AB$,交 AD 于点 M,交 BC 于点 N,$\therefore $四边形 ABNM 为矩形,$\therefore AB = MN = 8,AM = BN,∠AMN = ∠BNM = 90^{\circ }$.设$A'M = x$,则$A'N = 8 - x$.设$BN = y$,则$PM = y - 2$.在$Rt△PMA'$中,$PM^{2}+A'M^{2}=PA'^{2},\therefore (y - 2)^{2}+x^{2}=2^{2}$①.在$Rt△BNA'$中,$BN^{2}+A'N^{2}=A'B^{2},\therefore y^{2}+(8 - x)^{2}=8^{2}$②.由①②可得,$y = 4x$.把$y = 4x$代入①,得$(4x - 2)^{2}+x^{2}=2^{2}$,解得$x = \frac{16}{17}$或$x = 0$(舍去),$\therefore A'N = 8 - \frac{16}{17}=\frac{120}{17},\therefore S_{△A'BC}=\frac{1}{2}×BC×A'N=\frac{1}{2}×10×\frac{120}{17}=\frac{600}{17}$.