《2025年名校题库八年级数学上册北师大版》

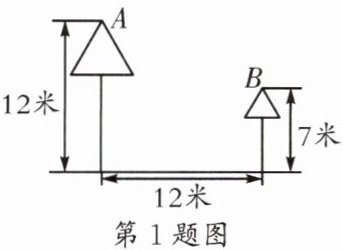
1. (高新区期末)如图,有两棵树,一棵高12米,另一棵高7米,两树相距12米,一只小鸟从一棵树的树梢A飞到另一棵树的树梢B,则小鸟至少要飞行13米。

答案： 解：过点B作BC垂直于较高树的底部，垂足为C。
则AC = 12 - 7 = 5米，BC = 12米。
在Rt△ABC中，AB² = AC² + BC² = 5² + 12² = 25 + 144 = 169，
所以AB = 13米。
13

2. (七中育才)如图,$∠AOB= 90^{\circ },OA= 25m,OB= 5m$,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球。如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是______m。

13

答案： 解：设机器人行走的路程 $ BC = x $ m，
因为小球滚动的速度与机器人行走的速度相等，运动时间相同，所以小球滚动的路程 $ AC = BC = x $ m。
已知 $ OA = 25 $ m，则 $ OC = OA - AC = (25 - x) $ m。
在 $ Rt\triangle BOC $ 中，$ \angle BOC = 90^\circ $，$ OB = 5 $ m，由勾股定理得：$ OB^2 + OC^2 = BC^2 $，
即 $ 5^2 + (25 - x)^2 = x^2 $，
解得 $ x = 13 $。
13

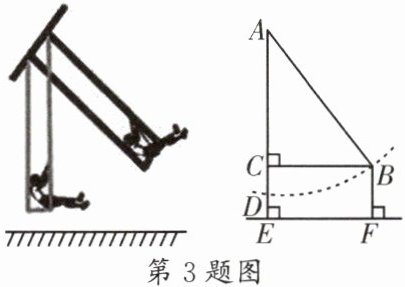
3. (武侯区期末)如图,一架秋千静止时,踏板离地的垂直高度$DE= 0.5m$,将它往前推送1.5m(水平距离$BC= 1.5m$)时,秋千的踏板离地的垂直高度$BF= 1m$,秋千的绳索始终拉直,则绳索AD的长是______m。

2.5

答案： 解：设绳索AD的长为$x$m。
因为$BF⊥EF$，$AE⊥EF$，$BC⊥AE$，所以四边形BCEF是矩形，$\triangle ACB$是直角三角形。
所以$CE = BF = 1m$，则$CD = CE - DE = 1 - 0.5 = 0.5m$。
又因为$AB = AD = x$m，所以$AC = AD - CD = (x - 0.5)m$。
在$Rt\triangle ABC$中，由勾股定理得$AC^2 + BC^2 = AB^2$，即$(x - 0.5)^2 + 1.5^2 = x^2$。
解得$x = 2.5$。
答：绳索AD的长是$2.5$m。
$2.5$

4. (实外西区)课间,小明拿着老师的等腰三角板玩,不小心掉到了两墙之间,如图所示。
(1)求证：$△ADC\cong △CEB;$
(2)从三角板的刻度可知$AC= 25cm$,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等)。

答案：
(1)证明：
∵∠ADC = ∠ACB = ∠CEB = 90°，
∴∠ACD + ∠BCE = 90°，∠DAC + ∠ACD = 90°，
∴∠BCE = ∠DAC.在△ADC和△CEB中，$\begin{cases}∠DAC = ∠BCE,\\∠ADC = ∠CEB,\\AC = BC,\end{cases}$
∴△ADC≌△CEB(AAS).
(2)解：由已知，得AD = 4a，BE = 3a.由
(1)知CE = AD = 4a，
∴在Rt△CEB中，$(3a)^2 + (4a)^2 = 25^2$，解得a = 5或a = -5(舍去)，
∴a = 5cm.

5. (石室联中)如图,明明在距离水面高度为5米的岸边C处,用绳子拉船靠岸,开始时绳子BC的长为13米。若明明收绳6米后,船到达D处,则船向岸A移动了多少米?

答案： 解：由题意得，CA⊥AB，∠CAB=90°，AC=5米，BC=13米。
收绳6米后，CD=BC - 6=13 - 6=7米。
在Rt△ABC中，AB=$\sqrt{BC^2 - AC^2}=\sqrt{13^2 - 5^2}=\sqrt{169 - 25}=\sqrt{144}=12$米。
在Rt△ADC中，AD=$\sqrt{CD^2 - AC^2}=\sqrt{7^2 - 5^2}=\sqrt{49 - 25}=\sqrt{24}=2\sqrt{6}$米。
∴BD=AB - AD=12 - 2$\sqrt{6}$米。
答：船向岸A移动了（12 - 2$\sqrt{6}$）米。