《2025年名校题库八年级数学上册北师大版》

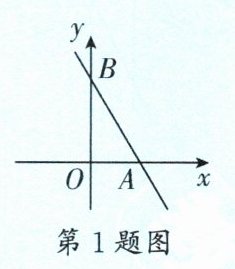
1. (金牛区期末)如图,直线$y= -\frac {4}{3}x+4$与x轴、y轴分别交于点A,B,M是y轴上一点,若将$\triangle ABM$沿AM折叠,点B恰好落在x轴上,则点M的坐标为____.

答案：
$(0,\frac {3}{2})$或$(0,-6)$【解析】设沿直线$AM$将$\triangle ABM$折叠,点$B$正好落在$x$轴上的点$C$处,则有$AB=AC$.由题意易得点$A(3,0)$,$B(0,4)$.当点$C$在直线$AB$的左侧时,如图1,$\because OA=3$,$OB=4$,$\therefore AB=5$,$\therefore$点$C$的坐标为$(-2,0)$.设点$M$的坐标为$(0,b)$,则$CM=BM=4-b$.$\because CM^{2}=CO^{2}+OM^{2}$,即$(4-b)^{2}=2^{2}+b^{2}$,$\therefore b=\frac {3}{2}$,$\therefore M(0,\frac {3}{2})$.当点$C$在直线$AB$的右侧时,如图2,同理求得$M(0,-6)$.

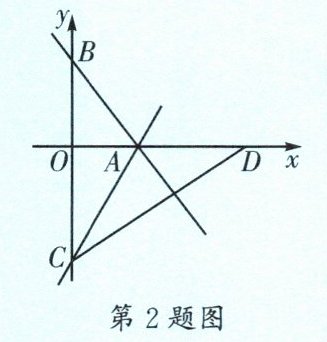
2. (西川)如图,在平面直角坐标系xOy中,直线$y= -\frac {4}{3}x+4$与x轴、y轴分别交于点A和点B,点C在y轴的负半轴上,将$\triangle ABC$沿AC翻折,点B恰好落在x轴正半轴上的点D处,点E在直线AC上,若点E到$\triangle COD的三边的距离之和等于\triangle COD$周长的一半,则点E的坐标为____.

$(4.5,3)$或$(-1.5,-9)$

答案： 解：对于直线$y=-\frac{4}{3}x+4$，当$x=0$时，$y=4$；当$y=0$时，$x=3$，则$A(3,0)$，$B(0,4)$，$OA=3$，$OB=4$。
由勾股定理得$AB=\sqrt{OA^2+OB^2}=5$，翻折后$AD=AB=5$，$OD=OA+AD=8$，$D(8,0)$。
设$C(0,t)(t＜0)$，则$BC=4-t$，$DC=\sqrt{t^2+8^2}$，由$BC=DC$得$4-t=\sqrt{t^2+64}$，解得$t=-6$，$C(0,-6)$。
设直线$AC$：$y=kx+b$，代入$A(3,0)$，$C(0,-6)$得$\begin{cases}3k+b=0\\b=-6\end{cases}$，解得$\begin{cases}k=2\\b=-6\end{cases}$，直线$AC$：$y=2x-6$。
设$E(a,2a-6)$，点$E$到$y$轴距离$|a|$，到$x$轴距离$|2a-6|$，由翻折性质知点$E$到$CD$距离等于到$y$轴距离$|a|$，则点$E$到$\triangle COD$三边距离之和为$2|a|+|2a-6|$。
在$Rt\triangle COD$中，$OC=6$，$OD=8$，$CD=10$，周长为$6+8+10=24$，则$2|a|+|2a-6|=12$。
分情况讨论：
①当$a＞0$，$2a-6＞0$（$a＞3$）时，$2a+2a-6=12$，解得$a=4.5$，$E(4.5,3)$；
②当$a＜0$，$2a-6＜0$（$a＜0$）时，$-2a-(2a-6)=12$，解得$a=-1.5$，$E(-1.5,-9)$；
③当$0＜a＜3$时，$2a-(2a-6)=6\neq12$，无解。
综上，点$E$的坐标为$(4.5,3)$或$(-1.5,-9)$。
$(4.5,3)$或$(-1.5,-9)$

3. (青羊区期末)如图,长方形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为$(-2,2\sqrt {3})$,E是BC的中点,点H在线段OA上,且$AH= \frac {1}{2}$,过点H且平行于y轴的HG与EB交于点G,现将长方形折叠,使顶点C落在HG上,并与HG上的点D重合,折痕为EF,F为折痕与y轴的交点.
(1)求$∠CEF$的度数和点D的坐标.
(2)求折痕EF所在直线的函数表达式.
(3)若点P在直线EF上,当$\triangle PFD$为等腰三角形时,试问:满足条件的点P有几个? 请求出点P的坐标,并写出解答过程.

答案： 解:
(1)$\because E$是$BC$的中点,$\therefore EC=EB=\frac {2}{2}=1$.由折叠的性质可得$\triangle FCE\cong \triangle FDE$,$\therefore ED=EC=1$,$∠FCE=∠FDE=90^{\circ }$,$DF=CF$.由题意,得$GH=AB=2\sqrt {3}$,$BG=AH=\frac {1}{2}$,$\therefore EG=EB-BG=1-\frac {1}{2}=\frac {1}{2}$.$\because$在$Rt\triangle DEG$中,$\frac {EG}{ED}=\frac {1}{2}$,$\therefore ∠EDG=30^{\circ }$,$\therefore ∠GED=60^{\circ }$,$\therefore ∠DEC=180^{\circ }-60^{\circ }=120^{\circ }$.$\because ∠DEF=∠CEF$,$\therefore ∠CEF=60^{\circ }$.在$Rt\triangle GED$中,由勾股定理,得$DG^{2}=ED^{2}-EG^{2}=1-\frac {1}{4}=\frac {3}{4}$,$\therefore DG=\frac {\sqrt {3}}{2}$,$\therefore DH=GH-DG=2\sqrt {3}-\frac {\sqrt {3}}{2}=\frac {3\sqrt {3}}{2}$.又$\because OH=OA-AH=2-\frac {1}{2}=\frac {3}{2}$,$\therefore D(-\frac {3}{2},\frac {3\sqrt {3}}{2})$.
(2)$\because ∠CEF=60^{\circ }$,$∠ECF=90^{\circ }$,$\therefore ∠CFE=30^{\circ }$,$\therefore EF=2CE=2$,$\therefore CF=\sqrt {EF^{2}-CE^{2}}=\sqrt {3}$,$\therefore OF=OC-CF=2\sqrt {3}-\sqrt {3}=\sqrt {3}$,$\therefore F(0,\sqrt {3})$.由
(1)可知,$E(-1,2\sqrt {3})$.设折痕$EF$所在直线的函数表达式为$y=kx+b$,则$\begin{cases} \sqrt {3}=b\\ 2\sqrt {3}=-k+b \end{cases}$,解得$\begin{cases} k=-\sqrt {3}\\ b=\sqrt {3} \end{cases}$,故折痕$EF$所在直线的函数表达式为$y=-\sqrt {3}x+\sqrt {3}$.
(3)$\because DF=CF=\sqrt {3}$,点$P$在直线$EF$上,$\therefore$当$\triangle PFD$为等腰三角形时,有以下三种情况:①当$PF=DF=\sqrt {3}$时,$PF^{2}=3$,令$P(t,-\sqrt {3}t+\sqrt {3})$,则$(t-0)^{2}+(-\sqrt {3}t+\sqrt {3}-\sqrt {3})^{2}=3$,$\therefore t^{2}+3t^{2}=3$,$\therefore t^{2}=\frac {3}{4}$,$\therefore t_{1}=-\frac {\sqrt {3}}{2}$,$t_{2}=\frac {\sqrt {3}}{2}$,此时点$P$的坐标为$(-\frac {\sqrt {3}}{2},\frac {2\sqrt {3}+3}{2})$或$(\frac {\sqrt {3}}{2},\frac {2\sqrt {3}-3}{2})$.②当$PD=DF=\sqrt {3}$时,$PD^{2}=3$,仍令$P(t,-\sqrt {3}t+\sqrt {3})$,则$(t+\frac {3}{2})^{2}+(-\sqrt {3}t+\sqrt {3}-\frac {3\sqrt {3}}{2})^{2}=3$,$\therefore t^{2}+3t+\frac {9}{4}+3t^{2}+3t+\frac {3}{4}=3$,$\therefore 4t^{2}+6t=0$,$\therefore t_{1}=0$,$t_{2}=-\frac {3}{2}$.当$t=0$时,点$P$与点$F$重合,不构成三角形,故舍去,此时点$P$的坐标为$(-\frac {3}{2},\frac {5\sqrt {3}}{2})$.③当$PD=PF$时,$PD^{2}=PF^{2}$,仍令$P(t,-\sqrt {3}t+\sqrt {3})$,则$(t+\frac {3}{2})^{2}+(-\sqrt {3}t+\sqrt {3}-\frac {3\sqrt {3}}{2})^{2}=(t-0)^{2}+(-\sqrt {3}t+\sqrt {3}-\sqrt {3})^{2}$,$\therefore t^{2}+3t+\frac {9}{4}+3t^{2}+3t+\frac {3}{4}=t^{2}+3t^{2}$,$\therefore 6t+3=0$,$\therefore t=-\frac {1}{2}$,此时点$P$的坐标为$(-\frac {1}{2},\frac {3\sqrt {3}}{2})$.综上所述,满足条件的点$P$有$4$个,分别是$(-\frac {\sqrt {3}}{2},\frac {2\sqrt {3}+3}{2})$,$(\frac {\sqrt {3}}{2},\frac {2\sqrt {3}-3}{2})$,$(-\frac {3}{2},\frac {5\sqrt {3}}{2})$,$(-\frac {1}{2},\frac {3\sqrt {3}}{2})$.