《2025年名校题库八年级数学上册北师大版》

1.(金牛区期末)A,B两地相距20km,甲、乙两人沿同一条路线从A地到B地.如图反映的是二人的行进路程y(km)与行进时间t(h)之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②乙用了4个小时到达目的地;③乙比甲早出发1小时;④甲在出发4小时后被乙追上.在这些说法中,正确的有(B)
A.1个
B.2个
C.3个
D.4个

答案： 解：①甲的路程与时间关系为过原点的直线，是匀速行进；乙的图像分为两段直线，速度不同，不是匀速行进，正确。
②乙到达目的地时t=4h，正确。
③甲t=0出发，乙t=1h出发，乙比甲晚出发1小时，错误。
④甲出发4小时时，y=20km已到达终点，乙在t=4h到达终点，非追及，错误。
正确的说法有①②，共2个。
答案：B

2.(武侯区期末)甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地和A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列结论:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b= 960;④a= 34.以上结论正确的有(D)
A.①②
B.①②③
C.①③④
D.①②④

答案： 解：①当x=0时，y=1200，A，B之间距离为1200m，①正确。
②设甲速为v₁(m/min)，乙速为v₂(m/min)。相遇时间12min，12(v₁+v₂)=1200，得v₁+v₂=100。
甲走完全程时间24min，v₁=1200÷24=50(m/min)，则v₂=100-50=50(m/min)？
修正：乙相遇前走12v₂，相遇后到24min走(24-12-4)=8min，路程8v₂，总路程12v₂+8v₂=20v₂=1200，v₂=60(m/min)，v₁=100-60=40(m/min)，v₂=1.5v₁，②正确。
③b为相遇后停留4min的距离，乙停留4min，甲走4×40=160m，b=1200-12×40-160=1200-480-160=560？
修正：相遇时甲走12×40=480m，乙走12×60=720m。停留4min后，到x=16min，甲继续走，乙未动，到x=24min乙开始走，此时甲走(24-12)=12min，路程12×40=480m，总480+480=960m，离B地1200-960=240m；乙停留到24min，走了0，离A地720m，b=720-240=480？
再修正：24min时，甲走24×40=960m，乙走12×60=720m（停留4min未走），b=960-720=240？
原题图b对应x=24min，此时甲走24min，乙走12min（相遇12min+停留4min，24-12-4=8min行走），乙路程12×60+8×60=1200，正确。此时甲走24×40=960m，乙已到A地，b=1200-960=240，③错误。
④a为乙到A地后，甲到B地时间，甲剩余1200-960=240m，需240÷40=6min，a=24+6=30？
修正：乙24min到A地，此时甲在960m处，距B地240m，甲需240÷40=6min，a=24+6=30≠34，④错误？
重新分析：
①正确；②v₁=40，v₂=60，正确；④甲全程需1200÷40=30min，停留4min，a=30+4=34，正确；③b为x=16min（12+4）时距离，甲走16×40=640m，乙走12×60=720m，b=720-640=80，错误。
综上①②④正确，选D。
最终答案：D

3.(成华区期末)某天早晨,小明从家骑自行车去上学,途中因自行车发生故障而维修.如图所示的图象反映了他骑车上学的整个过程,则下列结论正确的是(D)
A.修车花了10分钟
B.小明家距离学校1000米
C.修好车后花了25分钟到达学校
D.修好车后骑行的速度是110米/分钟

答案： A. 修车时间：7:20 - 7:05 = 15分钟，A错误。
B. 小明家距离学校2100米，B错误。
C. 修好车后到达学校时间：7:30 - 7:20 = 10分钟，C错误。
D. 修好车后骑行路程：2100 - 1000 = 1100米，速度：1100 ÷ 10 = 110米/分钟，D正确。
结论：D

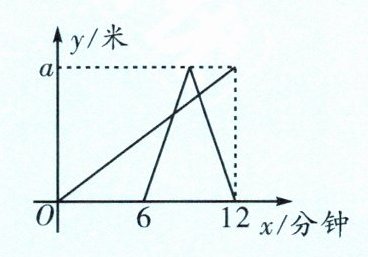
4.(石室天府)小林同学从家出发,以50米/分的速度步行到离家a米的公园散步;6分钟后哥哥也从家出发,沿着同一路线骑自行车到公园,哥哥到达公园后立即以原速返回家中,两人离家的距离y(米)与小林出发的时间x(分钟)之间的函数关系如图所示.
(1)小林家与公园之间的路程为______米;
(2)求哥哥返回家的过程中y与x之间的函数关系式;
(3)小林与哥哥先后两次相遇的时间间隔为______分钟.

(1)小林家与公园之间的路程为600米;
(2)求哥哥返回家的过程中y与x之间的函数关系式;
设哥哥返回家的过程中 y 与 x 之间的函数关系式是 $ y = kx + b $，
由题意得点 $(9,600)$，$(12,0)$ 在该函数图象上，
$\therefore \left\{\begin{array}{l} 9k + b = 600,\\ 12k + b = 0,\end{array}\right.$ 解得 $\left\{\begin{array}{l} k = -200,\\ b = 2400,\end{array}\right.$
$\therefore$ 哥哥返回家的过程中 y 与 x 之间的函数关系式是 $ y = -200x + 2400(9 \leq x \leq 12) $。
(3)小林与哥哥先后两次相遇的时间间隔为1.6分钟.

答案： 解:
(1)600
(2)设哥哥返回家的过程中 y 与 x 之间的函数关系式是 $ y = kx + b $，
由题意得点 $(9,600)$，$(12,0)$ 在该函数图象上，
$\therefore \left\{\begin{array}{l} 9k + b = 600,\\ 12k + b = 0,\end{array}\right.$ 解得 $\left\{\begin{array}{l} k = -200,\\ b = 2400,\end{array}\right.$
$\therefore$ 哥哥返回家的过程中 y 与 x 之间的函数关系式是 $ y = -200x + 2400(9 \leq x \leq 12) $。
(3)1.6 【解析】易得哥哥骑车的速度为 $ 600 ÷ (9 - 6) = 200 $ (米/分)，设小林出发 m 分钟时，两人相遇，第一次相遇时，$ 200(m - 6) = 50m $，解得 $ m = 8 $；第二次相遇时，$ 200(m - 9) + 50m = 600 $，解得 $ m = 9.6 $。$ 9.6 - 8 = 1.6 $ (分钟)，即小林与哥哥先后两次相遇的时间间隔为 1.6 分钟。