《2025年名校题库八年级数学上册北师大版》

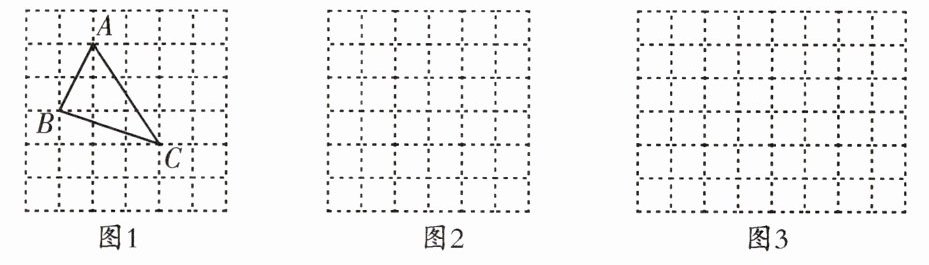
11. (高新区期末)问题背景：在$△ABC$中,AB,BC,AC三边的长分别为$\sqrt {5}$,$\sqrt {10}$,$\sqrt {13}$,求此三角形的面积.小辉同学在解答这道题时,先建立了一个正方形网格(每个小正方形的边长均为1),再在网格中画出格点$△ABC$(即$△ABC$三个顶点都在小正方形的顶点处),如图1所示.这样不需求$△ABC$的高,而借用网格就能计算出它的面积.
(1)请你求出$△ABC$的面积.
思维拓展：
(2)我们把上述求$△ABC$的面积的方法叫做构图法.如果$△ABC三边的长分别为\sqrt {5}a$,$\sqrt {10}a$,$\sqrt {17}a(a＞0)$,请利用图2的正方形网格(每个小正方形的边长均为a)画出相应的$△ABC$,并求出它的面积.
探索创新：
(3)若$△ABC三边的长分别为\sqrt {m^{2}+16n^{2}}$,$\sqrt {4m^{2}+9n^{2}}$,$\sqrt {9m^{2}+n^{2}}(m＞0,n＞0$,且$m≠n)$,试运用构图法在图3中画出示意图,并求出这个三角形的面积.

答案：
解:
(1)$△ABC$的面积为$3×3-\frac{1}{2}×3×1-\frac{1}{2}×3×2-\frac{1}{2}×1×2=\frac{7}{2}$。
(2)如图1，在边长为a的正方形网格中，$△ABC$即为所求作的三角形。
　　　　　　　　
　$△ABC$的面积为$2a\cdot 4a-\frac{1}{2}\cdot 2a\cdot a-\frac{1}{2}\cdot 3a\cdot a-\frac{1}{2}\cdot 4a\cdot a=\frac{7}{2}a^{2}$。
(3)如图2，在每个小长方形的长均为m、宽均为n的长方形网格中，$△ABC$即为所求作的三角形。
　　　　　　
　$△ABC$的面积为$3m\cdot 4n-\frac{1}{2}\cdot 3m\cdot n-\frac{1}{2}\cdot 2m\cdot 3n-\frac{1}{2}\cdot m\cdot 4n=\frac{11}{2}mn$。