《2025年名校题库八年级数学上册北师大版》

2. (石室联中)如图,在平面直角坐标系中有一长方形 $ ABCD $,其中 $ A(0,0) $,$ B(8,0) $,$ C(8,4) $,若将 $ \triangle ABC $ 沿 $ AC $ 所在的直线翻折,点 $ B $ 落在点 $ E $ 处,则点 $ E $ 的坐标是______。

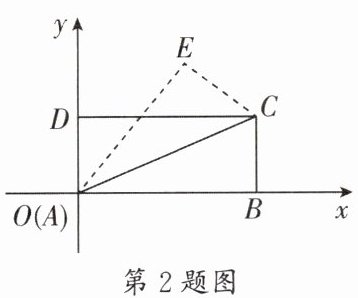
$(\frac{24}{5},\frac{32}{5})$

答案： 解：设点$E(x,y)$。
因为长方形$ABCD$中，$A(0,0)$，$B(8,0)$，$C(8,4)$，所以$AB=8$，$BC=4$。
由翻折性质知：$AE=AB=8$，$CE=CB=4$。
则$\begin{cases}x^{2}+y^{2}=8^{2} \\ (x - 8)^{2}+(y - 4)^{2}=4^{2}\end{cases}$
即$\begin{cases}x^{2}+y^{2}=64 ① \\ x^{2}-16x + 64 + y^{2}-8y + 16 = 16 ②\end{cases}$
将①代入②：$64 - 16x - 8y + 80 = 16$，化简得$2x + y = 16$，$y = 16 - 2x$。
代入①：$x^{2}+(16 - 2x)^{2}=64$，$x^{2}+256 - 64x + 4x^{2}=64$，$5x^{2}-64x + 192 = 0$。
解得$x = \frac{24}{5}$或$x = 8$（$x = 8$为点$B$，舍去）。
$y = 16 - 2×\frac{24}{5}=\frac{32}{5}$。
所以点$E$的坐标是$(\frac{24}{5},\frac{32}{5})$。
$(\frac{24}{5},\frac{32}{5})$

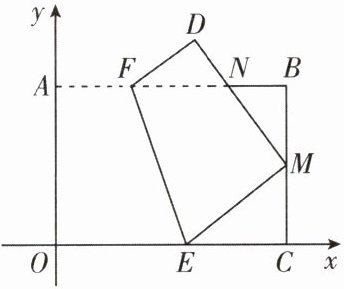
3. (高新区期末)如图,长方形 $ OABC $ 在平面直角坐标系中,点 $ B $ 的坐标为 $ (12,8) $,点 $ E,F $ 分别在 $ OC,AB $ 上,将四边形 $ A O E F $ 沿 $ EF $ 翻折,点 $ A $ 落在点 $ D $ 处,点 $ O $ 落在 $ BC $ 的中点 $ M $ 处,$ DM $ 与 $ AB $ 交于点 $ N $。
(1)求线段 $ EM $ 的长；
(2)求线段 $ AF $ 的长；
(3)直接写出点 $ D $ 的坐标。

答案：
解:
(1) $\because B(12,8)$,$\therefore AB = OC = 12 $,$ OA = BC = 8 $. 由折叠的性质可知,$ EM = OE $. 设 $ EM = x $, 则 $ OE = EM = x $,$ CE = OC - OE = 12 - x $.
∵M 是 BC 的中点,$\therefore CM = BM = \frac{1}{2}BC = 4 $. 在 $ Rt \triangle CEM $ 中, 由勾股定理,得 $ CE^{2} + CM^{2} = EM^{2} $, 即 $ (12 - x)^{2} + 4^{2} = x^{2} $, 解得 $ x = \frac{20}{3} $,$\therefore EM = \frac{20}{3} $.
(2) 如图, 连接 OF, FM. 设 $ AF = y $. 在 $ \triangle OEF $ 和 $ \triangle MEF $ 中, $\because \begin{cases} OE = EM, \\ \angle OEF = \angle MEF, \\ EF = EF, \end{cases} $$\therefore \triangle OEF \cong \triangle MEF(SAS) $,$\therefore OF = FM $,$\therefore AO^{2} + AF^{2} = BM^{2} + BF^{2} $,$\therefore 8^{2} + y^{2} = (12 - y)^{2} + 4^{2} $, 解得 $ y = 4 $, 即 $ AF = 4 $.
(3) 如图, 过点 D 作 $ DH \perp AB $ 于点 H, 易证 $ \triangle DFN \cong \triangle BMN $,$\therefore DN = BN $. 设 $ BN = DN = t $, 则 $ FN = AB - AF - BN = 12 - 4 - t = 8 - t $. 在 $ Rt \triangle FDN $ 中,$ DF^{2} + DN^{2} = FN^{2} $,$\therefore 4^{2} + t^{2} = (8 - t)^{2} $, 解得 $ t = 3 $,$\therefore DN = 3 $,$ FN = 5 $, 则 $ DH = \frac{FD \cdot DN}{FN} = \frac{12}{5} $. 在 $ Rt \triangle FDH $ 中,$ FH = \sqrt{FD^{2} - DH^{2}} = \frac{16}{5} $,$\therefore AH = AF + FH = 4 + \frac{16}{5} = \frac{36}{5} $,$\therefore D(\frac{36}{5}, \frac{52}{5}) $.

1.(高新区期末)在平面直角坐标系中,将点$A(-3,-2)$向右平移5个单位长度得到点$B$,则点$B关于y轴的对称点B'$的坐标为 (C)
A.$(2,2)$
B.$(-2,2)$
C.$(-2,-2)$
D.$(2,-2)$

答案： 解：将点$A(-3,-2)$向右平移5个单位长度，横坐标加5，纵坐标不变，得到点$B$的坐标为$(-3 + 5, -2) = (2, -2)$。
点$B(2, -2)$关于$y$轴的对称点$B'$，纵坐标不变，横坐标变为相反数，即$B'(-2, -2)$。
答案：C