《2025年名校题库八年级数学上册北师大版》

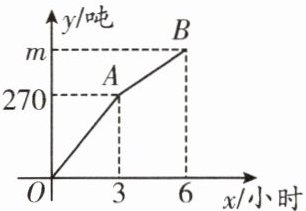
3.(武侯区期末)2017年8月8日在四川九寨沟县发生7.0级地震,习近平主席高度重视,立即作出重要指示,要求迅速组织力量救灾,最大限度减少人员伤亡.在本次救灾工作中,甲、乙两支清理队负责清理某路段的泥石,两支清理队同时工作3小时后,乙队被调往别处,留下甲队继续工作3小时后完成了剩余的清理任务.已知甲队每小时清理泥石40吨,乙队每小时清理泥石的量保持不变,甲、乙两队在此路段清理泥石的总量y(吨)与清理时间x(小时)之间的关系如图所示.
(1)试问:乙队每小时清理泥石多少吨? 请求出此次任务中甲、乙两队清理泥石的总量m的值.
(2)求y与x之间满足的函数关系式.

答案： 解:
(1)
∵甲队每小时清理泥石 40 吨,
∴乙队每小时清理泥石 $ 270 ÷ 3 - 40 = 50 $ (吨),
$ m = 270 + 40 × (6 - 3) = 390 $.
即乙队每小时清理泥石 50 吨,此次任务中甲、乙两队清理泥石的总量 $ m $ 的值是 390 吨.
(2)当 $ 0 \leq x \leq 3 $ 时,设 $ y $ 与 $ x $ 之间的函数关系式为 $ y = kx $,由 $ 270 = 3k $,解得 $ k = 90 $,即当 $ 0 \leq x \leq 3 $ 时,$ y $ 与 $ x $ 之间的函数关系式是 $ y = 90x $;当 $ 3 ＜ x \leq 6 $ 时,设 $ y $ 与 $ x $ 之间的函数关系式为 $ y = ax + b $,
![img alt=3-2]
易知 $ (3, 270) $ 满足关系式,则 $ \begin{cases} 3a + b = 270, \\ 6a + b = 390, \end{cases} $ 解得 $ \begin{cases} a = 40, \\ b = 150, \end{cases} $ 即当 $ 3 ＜ x \leq 6 $ 时,$ y $ 与 $ x $ 之间的函数关系式为 $ y = 40x + 150 $. 由上可得,$ y $ 与 $ x $ 之间的函数关系式为 $ y = \begin{cases} 90x(0 \leq x \leq 3), \\ 40x + 150(3 ＜ x \leq 6). \end{cases} $

4.(金牛区期末)某模具厂引进一种新机器,这种机器同一时间只能生产一种零件,每天只能工作8小时,每月工作25天.若一天用3小时生产A型零件、5小时生产B型零件,则共可生产34个零件;若一天用5小时生产A型零件、3小时生产B型零件,则共可生产30个零件.
(1)每小时可单独加工A型零件、B型零件各多少个?
(2)按市场统计,一个A型零件的利润是150元,一个B型零件的利润是100元,设该模具厂每月安排x(小时)生产A型零件,这两种零件所获得的总利润为y(元),试写出y与x的函数关系式(不要求写出自变量的取值范围).

答案： 解:
(1)设每小时可单独加工 $ A $ 型零件 $ m $ 个,$ B $ 型零件 $ n $ 个.
根据题意,得 $ \begin{cases} 3m + 5n = 34, \\ 5m + 3n = 30, \end{cases} $ 解得 $ \begin{cases} m = 3, \\ n = 5. \end{cases} $
答:每小时可单独加工 $ A $ 型零件 3 个,$ B $ 型零件 5 个.
(2)
∵这种机器每天只能工作 8 小时,每月工作 25 天,该模具厂每月安排 $ x $ (小时)生产 $ A $ 型零件,则每月安排 $ (25 × 8 - x) $ 小时生产 $ B $ 型零件.
由题意,得 $ y = 150 × 3x + 100 × 5(25 × 8 - x) = -50x + 100000 $,
∴ $ y $ 与 $ x $ 的函数关系式为 $ y = -50x + 100000 $.