《2025年名校题库八年级数学上册北师大版》

1. (金牛区期末)甲、乙两艘客轮同时离开港口,航行的速度都是 40 m/min,甲客轮用 15 min 到达点 A,乙客轮用 20 min 到达点 B. 若 A,B 两点的直线距离为 1000 m,甲客轮沿着北偏东 30°的方向航行,则乙客轮的航行方向可能是 (C)
A.北偏西 30°
B.南偏西 30°
C.南偏东 60°
D.南偏西 60°

答案： 解：甲客轮航行路程：$40×15 = 600$（m）
乙客轮航行路程：$40×20 = 800$（m）
$\because 600^{2}+800^{2}=360000 + 640000=1000000=1000^{2}$
$\therefore$甲、乙两客轮航线垂直。
甲沿北偏东$30^{\circ}$，则乙可能沿南偏东$60^{\circ}$（或北偏西$60^{\circ}$，选项中无北偏西$60^{\circ}$）
答案：C

2. (实外)如图,甲、乙两船从港口 A 同时出发,甲船以每小时 30 海里的速度向北偏东 35°方向航行,乙船以每小时 40 海里的速度向另一方向航行,1 小时后,甲船到达 C 岛,乙船到达 B 岛. 若 C,B 两岛相距 50 海里,请你求出乙船的航行方向.

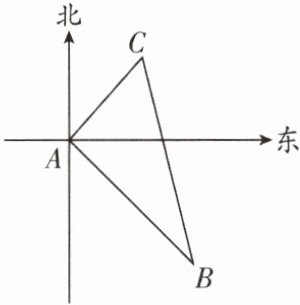
答案： 解：由题意得，甲船1小时行驶的距离AC=30×1=30海里，乙船1小时行驶的距离AB=40×1=40海里。
已知BC=50海里，因为30²+40²=900+1600=2500=50²，所以△ABC是直角三角形，∠BAC=90°。
甲船航行方向为北偏东35°，所以乙船与甲船的夹角为90°，则乙船与正东方向的夹角为90°-35°=55°，故乙船的航行方向为南偏东55°。

3. (成华区期末)如图,东西走向的 A,B 两座城市相距 100 千米,现计划要在两座城市之间修筑一条高等级公路(即线段 AB). 经测量,森林保护区的中心点 P 在 A 城市的北偏东 30°方向,B 城市的北偏西 45°方向上. 已知森林保护区的范围在以点 P 为圆心,50 千米为半径的圆形区域内. 请问：计划修筑的这条高等级公路会不会穿越森林保护区？为什么？

答案：
解:不会穿越森林保护区. 理由如下: 如图,过点P作PD⊥AB于点D. 设AD=x千米,则PD=√3x千米,BD=√3x千米,
∴√3x+x=100,即(√3+1)x=100,解得x=50(√3-1),
∴PD=(150-50√3)千米＞50千米,
∴不会穿越森林保护区.