《2025年名校题库八年级数学上册北师大版》

1. (青羊区期末)对于平面直角坐标系中的点$P(x,y)$,若$x,y满足|x-y|= 5$,则点$P(x,y)$就称为“平衡点”. 例如:$(1,6)$,因为$|1-6|= 5$,所以$(1,6)$是“平衡点”. 已知一次函数$y= 3x+k$($k$为常数)图象上有一个“平衡点”的坐标是$(3,8)$,则一次函数$y= 3x+k$($k$为常数)图象上另一个“平衡点”的坐标是______(-2,-7).

答案： 解：
∵点$(3,8)$是一次函数$y=3x+k$图象上的“平衡点”，
∴将$(3,8)$代入$y=3x+k$，得$8=3×3+k$，
解得$k=8 - 9 = -1$，
∴一次函数解析式为$y=3x - 1$。
∵点$P(x,y)$是“平衡点”，
∴$|x - y|=5$，又$y=3x - 1$，
∴$|x - (3x - 1)|=5$，即$| - 2x + 1|=5$，
则$-2x + 1 = 5$或$-2x + 1 = -5$。
当$-2x + 1 = 5$时，$-2x = 4$，解得$x = -2$，
此时$y=3×(-2) - 1 = -7$；
当$-2x + 1 = -5$时，$-2x = -6$，解得$x = 3$（已知点，舍去）。
∴另一个“平衡点”的坐标是$(-2,-7)$。
答案：$(-2,-7)$

2. (双流区期末)当$a,b$都是正实数,且满足等式$a-b= ab$时,我们称点$M(a,\frac {a}{b})$为“特异点”. 已知点$A(3,8)与点B都在直线y= -x+m$上,且点$B$是“特异点”,则$AB= $$2\sqrt{2}$.

答案： 解：
∵a,b是正实数且a−b=ab，
∴等式两边同除以b得：$\frac{a}{b}-1=a$，即$\frac{a}{b}=a+1$，
∴“特异点”M(a,$\frac{a}{b}$)可表示为(a,a+1)，即“特异点”在直线y=x+1上。
∵点A(3,8)在直线y=−x+m上，
∴8=−3+m，解得m=11，
∴直线AB的解析式为y=−x+11。
设点B为“特异点”，则B(n,n+1)，
又
∵点B在直线y=−x+11上，
∴n+1=−n+11，解得n=5，
∴B(5,6)。
∵A(3,8)，B(5,6)，
∴AB=$\sqrt{(5-3)^2+(6-8)^2}=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$。
答案：$2\sqrt{2}$

3. (天府新区期末)定义:若实数$a,b满足|2a-b|= k$($k$为常数),则称点$P(a,b)$为“$k$倍幸福点”. 如:点$P(2,1)$为“3倍幸福点”. 在平面直角坐标系$xOy$中,点$A(3,6)$,$B为直线l:y= x+m$上两点,其中点$B$为“$k$倍幸福点”,且$\triangle AOB的面积为3k-1$,则$k$的值为______$\frac{2}{3}$.

答案： 解：
∵点$A(3,6)$在直线$l:y = x + m$上，
∴$6 = 3 + m$，解得$m = 3$，
∴直线$l$的解析式为$y = x + 3$。
∵点$B$在直线$l:y = x + 3$上，
∴设点$B(n, n + 3)$。
∵点$B$为“$k$倍幸福点”，
∴$|2n - (n + 3)| = k$，即$|n - 3| = k$。
设直线$l:y = x + 3$与$y$轴交于点$C$，
令$x = 0$，则$y = 3$，
∴$C(0, 3)$，$OC = 3$。
∵$S_{\triangle AOB} = 3k - 1$，且$A(3,6)$，$B(n, n + 3)$，
$S_{\triangle AOB} = \frac{1}{2} × OC × |n - 3| = \frac{1}{2} × 3 × k$，
∴$\frac{1}{2} × 3k = 3k - 1$，
解得$k = \frac{2}{3}$。
故答案为$\frac{2}{3}$。

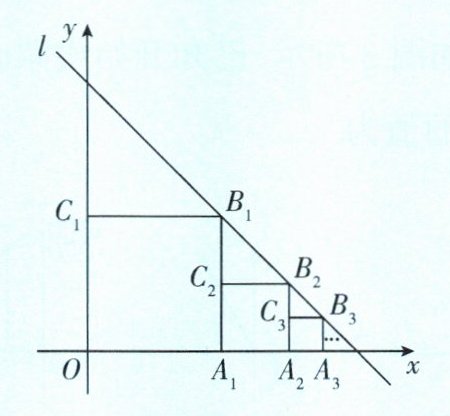
4. (武侯区期末)如图,已知直线$l:y= -x+4$,在直线$l上取点B_{1}$,过点$B_{1}分别向x$轴、$y$轴作垂线,交$x轴于点A_{1}$,交$y轴于点C_{1}$,使四边形$OA_{1}B_{1}C_{1}$为正方形;在直线$l上取点B_{2}$,过点$B_{2}分别向x$轴、$A_{1}B_{1}$作垂线,交$x轴于点A_{2}$,交$A_{1}B_{1}于点C_{2}$,使四边形$A_{1}A_{2}B_{2}C_{2}$为正方形;按此方法在直线$l上顺次取点B_{3},B_{4},...,B_{n}$,依次作正方形$A_{2}A_{3}B_{3}C_{3},A_{3}A_{4}B_{4}C_{4},...,A_{n-1}A_{n}B_{n}C_{n}$,则点$A_{3}$的坐标为______,点$B_{5}$的坐标为______.

答案：
($\frac{7}{2}$,0)　($\frac{31}{8}$,$\frac{1}{8}$)　[解析]如图,对y=−x+4,当x=0时,y=4;当y=0时,−x+4=0,解得x=4,
∴OE=OF=4,
∴△EOF是等腰直角三角形,
∴∠C1EF=45°,
∴△B1C1E是等腰直角三角形,
∴B1C1=EC1.
∵四边形OA1B1C1为正方形，
∴OC1=C1B1=EC1=2,
∴B1(2,2),A1(2,0).同理可得,C2是A1B1的中点，
∴B2(2 + 1 = 3,1),A2(3,0),B3(3+$\frac{1}{2}$=$\frac{7}{2}$,$\frac{1}{2}$),A3($\frac{7}{2}$,0),B4($\frac{7}{2}$+$\frac{1}{4}$=$\frac{15}{4}$,$\frac{1}{4}$),A4($\frac{15}{4}$,0),B5($\frac{15}{4}$+$\frac{1}{8}$=$\frac{31}{8}$,$\frac{1}{8}$).