第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
6.(武侯区期末)
[阅读理解]
如图,在$\triangle ABC$中,$AB= 4,AC= 6,BC= 7$,过点A作直线BC的垂线,垂足为D,求线段AD的长.
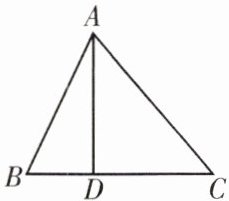
解:设$BD= x$,则$CD= 7-x.\because AD⊥BC,\therefore ∠ADB= ∠ADC= 90^{\circ }$.
在$Rt\triangle ABD$中,$AD^{2}= AB^{2}-BD^{2}$,在$Rt\triangle ACD$中,$AD^{2}= AC^{2}-CD^{2},\therefore AB^{2}-BD^{2}= AC^{2}-CD^{2}$.
又$\because AB= 4,AC= 6,\therefore 4^{2}-x^{2}= 6^{2}-(7-x)^{2}$,解得$x= \frac {29}{14}$,
$\therefore BD= \frac {29}{14},\therefore AD= \sqrt {AB^{2}-BD^{2}}= \frac {3\sqrt {255}}{14}$.
[知识迁移]
(1)在$\triangle ABC$中,$AB= 13,AC= 15$,过点A作直线BC的垂线,垂足为D.
①如图1,若$BC= 14$,求线段AD的长;
②若$AD= 12$,求线段BC的长.
(2)如图2,在$\triangle ABC$中,$AB= \frac {25}{4}\sqrt {5},AC= \frac {5}{2}\sqrt {29}$,过点A作直线BC的垂线,交线段BC于点D,将$\triangle ABD$沿直线AB翻折后得到对应的$\triangle ABD'$,连接$CD'$,若$AD= \frac {25}{2}$,求线段$CD'$的长.
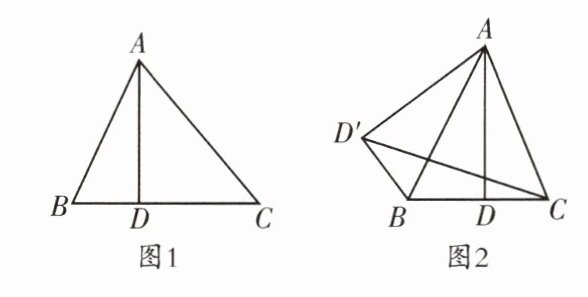
[阅读理解]
如图,在$\triangle ABC$中,$AB= 4,AC= 6,BC= 7$,过点A作直线BC的垂线,垂足为D,求线段AD的长.

解:设$BD= x$,则$CD= 7-x.\because AD⊥BC,\therefore ∠ADB= ∠ADC= 90^{\circ }$.
在$Rt\triangle ABD$中,$AD^{2}= AB^{2}-BD^{2}$,在$Rt\triangle ACD$中,$AD^{2}= AC^{2}-CD^{2},\therefore AB^{2}-BD^{2}= AC^{2}-CD^{2}$.
又$\because AB= 4,AC= 6,\therefore 4^{2}-x^{2}= 6^{2}-(7-x)^{2}$,解得$x= \frac {29}{14}$,
$\therefore BD= \frac {29}{14},\therefore AD= \sqrt {AB^{2}-BD^{2}}= \frac {3\sqrt {255}}{14}$.
[知识迁移]
(1)在$\triangle ABC$中,$AB= 13,AC= 15$,过点A作直线BC的垂线,垂足为D.
①如图1,若$BC= 14$,求线段AD的长;
②若$AD= 12$,求线段BC的长.
(2)如图2,在$\triangle ABC$中,$AB= \frac {25}{4}\sqrt {5},AC= \frac {5}{2}\sqrt {29}$,过点A作直线BC的垂线,交线段BC于点D,将$\triangle ABD$沿直线AB翻折后得到对应的$\triangle ABD'$,连接$CD'$,若$AD= \frac {25}{2}$,求线段$CD'$的长.

答案:
解:
(1)①设BD = x,则CD = 14 - x.
∵AD⊥BC,
∴∠ADB = ∠ADC = 90°.在Rt△ABD中,AD² = AB² - BD²,在Rt△ACD中,AD² = AC² - CD²,
∴AB² - BD² = AC² - CD².
∵AB = 13,AC = 15,
∴13² - x² = 15² - (14 - x)²,
∴x = 5,
∴BD = 5,
∴AD = $\sqrt{AB^{2} - BD^{2}}$ = $\sqrt{13^{2} - 5^{2}}$ = 12. ②在Rt△ABD中,BD = $\sqrt{AB^{2} - AD^{2}}$ = $\sqrt{13^{2} - 12^{2}}$ = 5.在Rt△ACD中,CD = $\sqrt{AC^{2} - AD^{2}}$ = $\sqrt{15^{2} - 12^{2}}$ = 9.当∠ABC为锐角时,如图1,BC = BD + CD = 5 + 9 = 14,当∠ABC为钝角时,如图2,BC = CD - BD = 9 - 5 = 4.


(2)如图3,连接DD'交AB于点N,则DD'⊥AB,过点D'作D'H⊥BD交DB的延长线于点H.在Rt△ABD中,BD = $\sqrt{AB^{2} - AD^{2}}$ = $\sqrt{(\frac{25}{4}\sqrt{5})^{2} - (\frac{25}{2})^{2}}$ = $\frac{25}{4}$.在Rt△ACD中,CD = $\sqrt{AC^{2} - AD^{2}}$ = $\sqrt{(\frac{5}{2}\sqrt{29})^{2} - (\frac{25}{2})^{2}}$ = 5.
∵AB垂直平分DD',
∴D'B = DB = $\frac{25}{4}$,D'D = 2DN.
∵$S_{\triangle ABD}$ = $\frac{1}{2}$AD·BD = $\frac{1}{2}$AB·DN,
∴$\frac{25}{2}×\frac{25}{4} = \frac{25}{4}\sqrt{5} \cdot DN$,
∴DN = $\frac{5\sqrt{5}}{2}$,
∴D'D = 2DN = 5$\sqrt{5}$.设HB = m,则HD = HB + BD = m + $\frac{25}{4}$.
∵D'H² = D'D² - HD² = D'B² - HB²,
∴(5$\sqrt{5}$)² - (m + $\frac{25}{4}$)² = ($\frac{25}{4}$)² - m²,
∴m = $\frac{15}{4}$,
∴HB = $\frac{15}{4}$,
∴HC = HB + BD + CD = $\frac{15}{4} + \frac{25}{4} + 5 = 15$,$D'H = \sqrt{D'B^{2} - HB^{2}}$ = $\sqrt{(\frac{25}{4})^{2} - (\frac{15}{4})^{2}}$ = 5,
∴CD' = $\sqrt{D'H^{2} + HC^{2}}$ = $\sqrt{5^{2} + 15^{2}}$ = 5$\sqrt{10}$.
解:
(1)①设BD = x,则CD = 14 - x.
∵AD⊥BC,
∴∠ADB = ∠ADC = 90°.在Rt△ABD中,AD² = AB² - BD²,在Rt△ACD中,AD² = AC² - CD²,
∴AB² - BD² = AC² - CD².
∵AB = 13,AC = 15,
∴13² - x² = 15² - (14 - x)²,
∴x = 5,
∴BD = 5,
∴AD = $\sqrt{AB^{2} - BD^{2}}$ = $\sqrt{13^{2} - 5^{2}}$ = 12. ②在Rt△ABD中,BD = $\sqrt{AB^{2} - AD^{2}}$ = $\sqrt{13^{2} - 12^{2}}$ = 5.在Rt△ACD中,CD = $\sqrt{AC^{2} - AD^{2}}$ = $\sqrt{15^{2} - 12^{2}}$ = 9.当∠ABC为锐角时,如图1,BC = BD + CD = 5 + 9 = 14,当∠ABC为钝角时,如图2,BC = CD - BD = 9 - 5 = 4.


(2)如图3,连接DD'交AB于点N,则DD'⊥AB,过点D'作D'H⊥BD交DB的延长线于点H.在Rt△ABD中,BD = $\sqrt{AB^{2} - AD^{2}}$ = $\sqrt{(\frac{25}{4}\sqrt{5})^{2} - (\frac{25}{2})^{2}}$ = $\frac{25}{4}$.在Rt△ACD中,CD = $\sqrt{AC^{2} - AD^{2}}$ = $\sqrt{(\frac{5}{2}\sqrt{29})^{2} - (\frac{25}{2})^{2}}$ = 5.
∵AB垂直平分DD',
∴D'B = DB = $\frac{25}{4}$,D'D = 2DN.
∵$S_{\triangle ABD}$ = $\frac{1}{2}$AD·BD = $\frac{1}{2}$AB·DN,
∴$\frac{25}{2}×\frac{25}{4} = \frac{25}{4}\sqrt{5} \cdot DN$,
∴DN = $\frac{5\sqrt{5}}{2}$,
∴D'D = 2DN = 5$\sqrt{5}$.设HB = m,则HD = HB + BD = m + $\frac{25}{4}$.
∵D'H² = D'D² - HD² = D'B² - HB²,
∴(5$\sqrt{5}$)² - (m + $\frac{25}{4}$)² = ($\frac{25}{4}$)² - m²,
∴m = $\frac{15}{4}$,
∴HB = $\frac{15}{4}$,
∴HC = HB + BD + CD = $\frac{15}{4} + \frac{25}{4} + 5 = 15$,$D'H = \sqrt{D'B^{2} - HB^{2}}$ = $\sqrt{(\frac{25}{4})^{2} - (\frac{15}{4})^{2}}$ = 5,
∴CD' = $\sqrt{D'H^{2} + HC^{2}}$ = $\sqrt{5^{2} + 15^{2}}$ = 5$\sqrt{10}$.
查看更多完整答案,请扫码查看


