《2025年名校题库八年级数学上册北师大版》

1.(师大一中)已知有序数对$(a,b)及常数k$,我们称有序数对$(ka + b,a - b)为有序数对(a,b)$的“$k$阶结伴数对”.如$(3,2)$的“$1$阶结伴数对”为$(1×3 + 2,3 - 2)$,即$(5,1)$.若有序数对$(a,b)(b≠0)$与它的“$k$阶结伴数对”关于$y$轴对称,则此时$k$的值为(B)
A.$-2$
B.$-\frac{3}{2}$
C.$0$
D.$-\frac{1}{2}$

答案： 解：由题意得，有序数对$(a,b)$的“$k$阶结伴数对”为$(ka + b,a - b)$。
因为$(a,b)$与它的“$k$阶结伴数对”关于$y$轴对称，所以它们的横坐标互为相反数，纵坐标相等。
可得方程组：
$\begin{cases}ka + b = -a \\a - b = b\end{cases}$
由第二个方程$a - b = b$，得$a = 2b$。
将$a = 2b$代入第一个方程$ka + b = -a$，得：
$k \cdot 2b + b = -2b$
因为$b \neq 0$，两边同时除以$b$：
$2k + 1 = -2$
解得$2k = -3$，$k = -\frac{3}{2}$。
答案：B

2.(高新区期末)对于平面直角坐标系$xOy中的点P与图形M$,$N$给出如下定义:点$P到图形M上的各点的最小距离为m$,点$P到图形N上各点的最小距离为n$,当$m = n$时,称点$P为图形M与图形N$的“等长点”.如:点$E(-2,0)$,$O(0,0)$,$F(2,0)$中,点$O就是点E与点F$的“等长点”.已知点$A(2,0)$,$B(2,2)$,$C(2,-2)$,连接$BC$,若点$P既是点O与点A$的“等长点”,也是线段$OA与线段BC$的“等长点”,则点$P$的坐标为______(1,1)或(1,-1).

答案： 解：设点$P$的坐标为$(x,y)$。
情况1：点$P$是点$O$与点$A$的“等长点”
点$O(0,0)$，点$A(2,0)$，则点$P$到$O$的距离$m = \sqrt{x^2 + y^2}$，到$A$的距离$n = \sqrt{(x-2)^2 + y^2}$。
由$m = n$得：
$\sqrt{x^2 + y^2} = \sqrt{(x-2)^2 + y^2}$
两边平方化简得$x^2 = (x-2)^2$，解得$x = 1$。
情况2：点$P$是线段$OA$与线段$BC$的“等长点”
线段$OA$在$x$轴上，$0 \leq x \leq 2$，$y = 0$，点$P(1,y)$到$OA$的最小距离$m = |y|$。
线段$BC$：点$B(2,2)$，$C(2,-2)$，在直线$x = 2$上，$-2 \leq y \leq 2$，点$P(1,y)$到$BC$的最小距离$n = |1 - 2| = 1$。
由$m = n$得$|y| = 1$，解得$y = 1$或$y = -1$。
综上，点$P$的坐标为$(1,1)$或$(1,-1)$。
$(1,1)$或$(1,-1)$

3.(树德实验)在平面直角坐标系$xOy$中,一只青蛙从原点$O$出发,按向上、向右、向下、向右的方向依次跳动,每次跳动$2$个单位长度,其跳动路线如图所示,则点$A_{12}$的坐标为$(12,0)$,点$A_{2025}$的坐标为$(2024,2)$.

答案： 解：观察跳动路线可知，青蛙跳动的规律为每4次跳动为一个循环，每次循环向右移动4个单位长度。
对于点$A_{12}$：$12÷4 = 3$，刚好完成3个循环，每个循环向右移动4个单位，所以横坐标为$3×4 = 12$，纵坐标为0，即$A_{12}(12,0)$。
对于点$A_{2025}$：$2025÷4 = 506\cdots\cdots1$，即完成506个循环后，又跳动了1次。506个循环向右移动$506×4 = 2024$个单位，第2025次跳动方向为向上，纵坐标为2，所以$A_{2025}(2024,2)$。
答案：$(12,0)$；$(2024,2)$

4.(七中育才)如图,在平面直角坐标系$xOy$中,将等边$\triangle OAB绕点A旋转180^{\circ}得到\triangle O_1AB_1$,再将$\triangle O_1AB_1绕点O_1旋转180^{\circ}得到\triangle O_1A_1B_2$,再将$\triangle O_1A_1B_2绕点A_1旋转180^{\circ}得到\triangle O_2A_1B_3$,……,按此规律进行下去,若点$B的坐标为(-2,0)$,则点$B_{2024}$的坐标为______.

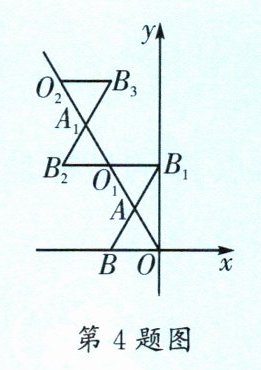
(-2026, 2024√3)

答案： 解：
∵△O₁AB₁由△OAB绕点A旋转180°得到，
∴点B，A，B₁共线，AB=AB₁。
∵△OAB是等边三角形，B(-2,0)，
∴OB=2，OA=AB=2，∠AOB=60°，
∴点A坐标为(-1, √3)。
由旋转性质得B₁坐标为(0, 2√3)。
∵△O₁A₁B₂由△O₁AB₁绕点O₁旋转180°得到，
∴O₁A=O₁A₁，O₁B₁=O₁B₂，
又O₁B₁//x轴，O₁B₁=2，
∴B₂坐标为(-4, 2√3)。
同理可得：
B₃(-2, 4√3)，B₄(-6, 4√3)，B₅(-4, 6√3)，B₆(-8, 6√3)，…
观察规律：当n为偶数时，Bₙ坐标为(-n-2, n√3)。
当n=2024时，
x=-2024-2=-2026，y=2024√3，
∴点B₂₀₂₄的坐标为(-2026, 2024√3)。
答案：(-2026, 2024√3)

5.(七中万达)如图,在平面直角坐标系$xOy$中,将$\triangle ABO绕点A按顺时针方向旋转到\triangle AB_1C_1$的位置,点$B$,$O分别落在点B_1$,$C_1$处,点$B_1在x$轴上,再将$\triangle AB_1C_1绕点B_1按顺时针方向旋转到\triangle A_1B_1C_2$的位置,点$C_2在x$轴上,再将$\triangle A_1B_1C_2绕点C_2按顺时针方向旋转到\triangle A_2B_2C_2$的位置,点$A_2在x$轴上,……依此规律进行下去.若点$A(\frac{5}{3},0)$,$B(0,4)$,则点$B_{2025}$的横坐标为______10126.

答案： 解：在$Rt\triangle ABO$中，$OA=\frac{5}{3}$，$OB=4$，
$AB=\sqrt{OA^2 + OB^2}=\sqrt{(\frac{5}{3})^2 + 4^2}=\frac{13}{3}$，
$\triangle ABO$周长为$OA + OB + AB=\frac{5}{3}+4+\frac{13}{3}=10$。
观察旋转规律：
- 当$n$为偶数时，$B_n$横坐标为$\frac{n}{2}×10$；
- 当$n$为奇数时，$B_n$横坐标为$\frac{n - 1}{2}×10+6$。
因为$2025$是奇数，
所以点$B_{2025}$的横坐标为$\frac{2025 - 1}{2}×10+6=10126$。
答案：$10126$