《2025年名校题库八年级数学上册北师大版》

1. (锦江区期末)《九章算术》中有一个“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问:折处高几尺?即:如图,$AB+AC= 9$尺,$BC= 3$尺,则$AC= $4尺.

答案： 解：设折处高 $ AC = x $ 尺，则 $ AB = (9 - x) $ 尺。
在 $ \text{Rt}\triangle ABC $ 中，$ AC^2 + BC^2 = AB^2 $，
即 $ x^2 + 3^2 = (9 - x)^2 $。
展开得 $ x^2 + 9 = 81 - 18x + x^2 $，
化简得 $ 18x = 72 $，解得 $ x = 4 $。
$ 4 $

2. (东部新区期末)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.在《九章算术》中的勾股卷中有这样一道题:今有竹高一丈,末折抵底,去本三尺.问折者高几何?意思为:如图,一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处B离远处竹子C的距离BC为3尺,则折断后的竹子$AC= $$\frac{91}{20}$尺.(注:1丈= 10尺)

答案： 解：设折断后的竹子 $ AC $ 为 $ x $ 尺，则斜边 $ AB $ 为 $ (10 - x) $ 尺。
在 $ Rt\triangle ABC $ 中，由勾股定理得：
$x^{2} + 3^{2} = (10 - x)^{2}$
展开并化简方程：
$x^{2} + 9 = 100 - 20x + x^{2}$
$20x = 91$
$x = \frac{91}{20}$
故折断后的竹子 $ AC = \frac{91}{20} $ 尺。
答案：$\frac{91}{20}$

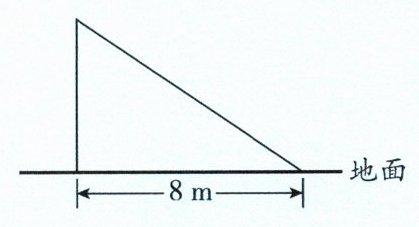
3. (西川)如图,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处.已知旗杆原长16米,请你求出旗杆是在离底部多少米的位置断裂的.

答案： 解:设旗杆是在离底部 $ x $ 米的位置断裂的,则断裂后顶部长度为 $ (16 - x) $ 米。
根据勾股定理可得 $ x^{2} + 8^{2} = (16 - x)^{2} $,
展开得 $ x^{2} + 64 = 256 - 32x + x^{2} $,
移项化简得 $ 32x = 192 $,
解得 $ x = 6 $。
答:旗杆是在离底部 6 米的位置断裂的。

1. (七中八一)在一次消防演习中,消防员架起一架25米长的云梯,斜靠在一面墙上,梯子底端C离墙20米,如图所示。
(1)这架梯子的顶端A距地面有多高？
(2)如果消防员接到命令,要求梯子的顶端上升4米(云梯长度不变),那么云梯底部在水平方向应滑动多少米？

答案： 1. 解:
(1) 由题意, 得 $ AC = 25 $ 米, $ BC = 20 $ 米, 则 $ AB = \sqrt { A C ^ { 2 } - B C ^ { 2 } } = \sqrt { 6 2 5 - 4 0 0 } = 1 5 $ (米). 故这架梯子的顶端 $ A $ 距地面有 $ 15 $ 米.
(2) 由题意, 得 $ E A = 4 $ 米, 则 $ B E = 1 9 $ 米, $ B D = \sqrt { D E ^ { 2 } - B E ^ { 2 } } = \sqrt { 6 2 5 - 3 6 1 } = 2 \sqrt { 6 6 } $ (米). $ \because B C = 2 0 $ 米, $ \therefore C D = ( 2 0 - 2 \sqrt { 6 6 } ) $ 米. 故云梯底部在水平方向应滑动 $ ( 2 0 - 2 \sqrt { 6 6 } ) $ 米.