第114页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
3. (石室联中)如图,已知直线$y= x-4分别与x$轴、$y轴交于A$,$B$两点,直线$OG:y= kx(k<0)交AB于点D$。
(1)求$A$,$B$两点的坐标。
(2)如图1,$E是线段OB$的中点,连接$AE$,$F是射线OG$上一点,当$OG⊥AE$,且$OF= AE$时,
①求$EF$的长;
②在$x轴上找一点P$,使$PE+PD$的值最小,求出点$P$的坐标。
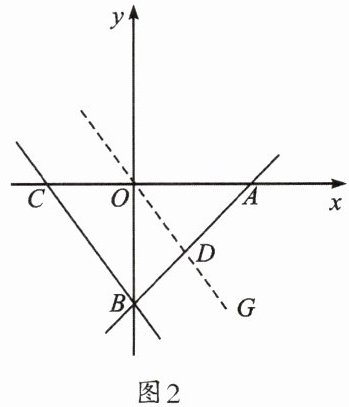
(3)如图2,若$k= -\frac {4}{3}$,过点$B作BC// OG$,交$x轴于点C$,此时在$x轴上是否存在点M$,使$∠ABM+∠CBO= 45^{\circ }$?若存在,求出点$M$的坐标;若不存在,请说明理由。
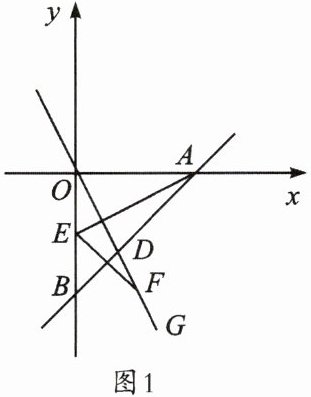
(1)求$A$,$B$两点的坐标。
(2)如图1,$E是线段OB$的中点,连接$AE$,$F是射线OG$上一点,当$OG⊥AE$,且$OF= AE$时,
①求$EF$的长;
②在$x轴上找一点P$,使$PE+PD$的值最小,求出点$P$的坐标。
(3)如图2,若$k= -\frac {4}{3}$,过点$B作BC// OG$,交$x轴于点C$,此时在$x轴上是否存在点M$,使$∠ABM+∠CBO= 45^{\circ }$?若存在,求出点$M$的坐标;若不存在,请说明理由。


答案:
3.解:
(1)
∵直线y=x-4分别与x轴、y轴交于A,B两点,
∴令y=0,则x-4=0,得x=4;
令x=0,则y=-4,
∴A(4,0),B(0,-4).
(2)①
∵A(4,0),B(0,-4),
∴OA=OB=4.
∵E是线段OB的中点,
∴OE=2.
如图1,过点F作FB'⊥y轴于点B',
∴∠AOE=∠OB'F=90°.
∵OG⊥AE,
∴∠OAE+∠AOF=∠BOG+∠AOF=90°,
∴∠OAE=∠B{OF.
又
∵OF=AE,
∴△AOE≌△OB'F(AAS),
∴FB=OE=2,OB'=OA=4.
∵OB=4,
∴点B与点B'重合,
∴EF=
$\sqrt{BE+BF}$=$\sqrt{2²+2²}$=2$\sqrt{2}$
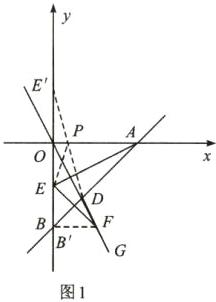
②由①可知,F(2,-4),
∴直线OF的解析式为y=-2x.
由{yy==x−−2x4,,解得x=$\frac{4}{3}$,,
∴D($\frac{4}{3}$,-$\frac{8}{3}${.
y=-$\frac{8}{3}$
如图1,作点E关于x轴的对称点E',连接DE交x轴于点P,连接PE,此时PE+PD的值最小、.
∵E(0,2),
∴直线DE的解析式为y=-$\frac{7}{2}$x+2,令y=0,得x=$\frac{4}{7}$,
∴P($\frac{4}{7}$,0).
(3)存在.
∵k=-$\frac{4}{3}$
∴直线OG:y=-$\frac{4}{3}$x.
∵BC//OG,
∴易得直线BC的解析式为y=
-$\frac{4}{3}$x-4.
当y=0时,即-$\frac{4}{3}$x-4=0,
∴x=-3,
∴C(-3,0).如图2,当点M在点A的左侧时,
∵∠ABO=
45°,∠ABM+∠CBO=45°,
∴∠MBO=∠CBO.又
∵∠COB=∠MOB=90°,OB=OB,
∴△BCO≌△BMO(ASA),
∴OM=OC=3,
∴M(3,0).当点M在点A的右侧时,记点M为点M',
∵∠OAB=∠AMB+∠ABM=45°,∠ABM+∠CBO=45°,
∴∠AM'B=∠OBC.
∵∠CBO=∠OMB,∠OMB+∠OBM=90°,
∴∠CBO+∠0BMr=90°.
设OM=a,
∴BM=$\sqrt{4²+a²}$
∵SCBM=$\frac{1}{2}$OB.CM=$\frac{1}{2}$BC.BMr,
∴4×(3+a)=$\sqrt{3²+4²}$×√4²+a²,
∴a=$\frac{16}{3}$,
∴M($\frac{16}{3}$,0).
综上所述,点M的坐标为((3,0)或($\frac{16}{3}$,o).

3.解:
(1)
∵直线y=x-4分别与x轴、y轴交于A,B两点,
∴令y=0,则x-4=0,得x=4;
令x=0,则y=-4,
∴A(4,0),B(0,-4).
(2)①
∵A(4,0),B(0,-4),
∴OA=OB=4.
∵E是线段OB的中点,
∴OE=2.
如图1,过点F作FB'⊥y轴于点B',
∴∠AOE=∠OB'F=90°.
∵OG⊥AE,
∴∠OAE+∠AOF=∠BOG+∠AOF=90°,
∴∠OAE=∠B{OF.
又
∵OF=AE,
∴△AOE≌△OB'F(AAS),
∴FB=OE=2,OB'=OA=4.
∵OB=4,
∴点B与点B'重合,
∴EF=
$\sqrt{BE+BF}$=$\sqrt{2²+2²}$=2$\sqrt{2}$

②由①可知,F(2,-4),
∴直线OF的解析式为y=-2x.
由{yy==x−−2x4,,解得x=$\frac{4}{3}$,,
∴D($\frac{4}{3}$,-$\frac{8}{3}${.
y=-$\frac{8}{3}$
如图1,作点E关于x轴的对称点E',连接DE交x轴于点P,连接PE,此时PE+PD的值最小、.
∵E(0,2),
∴直线DE的解析式为y=-$\frac{7}{2}$x+2,令y=0,得x=$\frac{4}{7}$,
∴P($\frac{4}{7}$,0).
(3)存在.
∵k=-$\frac{4}{3}$
∴直线OG:y=-$\frac{4}{3}$x.
∵BC//OG,
∴易得直线BC的解析式为y=
-$\frac{4}{3}$x-4.
当y=0时,即-$\frac{4}{3}$x-4=0,
∴x=-3,
∴C(-3,0).如图2,当点M在点A的左侧时,
∵∠ABO=
45°,∠ABM+∠CBO=45°,
∴∠MBO=∠CBO.又
∵∠COB=∠MOB=90°,OB=OB,
∴△BCO≌△BMO(ASA),
∴OM=OC=3,
∴M(3,0).当点M在点A的右侧时,记点M为点M',
∵∠OAB=∠AMB+∠ABM=45°,∠ABM+∠CBO=45°,
∴∠AM'B=∠OBC.
∵∠CBO=∠OMB,∠OMB+∠OBM=90°,
∴∠CBO+∠0BMr=90°.
设OM=a,
∴BM=$\sqrt{4²+a²}$
∵SCBM=$\frac{1}{2}$OB.CM=$\frac{1}{2}$BC.BMr,
∴4×(3+a)=$\sqrt{3²+4²}$×√4²+a²,
∴a=$\frac{16}{3}$,
∴M($\frac{16}{3}$,0).
综上所述,点M的坐标为((3,0)或($\frac{16}{3}$,o).

查看更多完整答案,请扫码查看


