第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
6.(石室联中)一个动点在第一象限及$x$轴、$y$轴上运动,在第一秒钟,它从原点$(0,0)运动到点(0,1)$,然后接着按图中箭头所示方向运动(即$(0,0)\to(0,1)\to(1,1)\to(1,0)…\to$),且每秒移动$1$个单位长度,那么第$100$秒时动点所在位置的坐标是______.
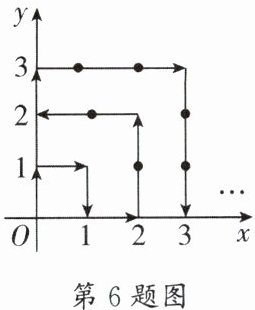

(10,0)
答案:
解:通过观察动点运动规律可得:
3秒时到了$(1,0)$,
8秒时到了$(0,2)$,
15秒时到了$(3,0)$,
24秒时到了$(0,4)$,
35秒时到了$(5,0)$,
48秒时到了$(0,6)$,
63秒时到了$(7,0)$,
80秒时到了$(0,8)$,
99秒时到了$(9,0)$,
100秒时到了$(10,0)$。
$(10,0)$
3秒时到了$(1,0)$,
8秒时到了$(0,2)$,
15秒时到了$(3,0)$,
24秒时到了$(0,4)$,
35秒时到了$(5,0)$,
48秒时到了$(0,6)$,
63秒时到了$(7,0)$,
80秒时到了$(0,8)$,
99秒时到了$(9,0)$,
100秒时到了$(10,0)$。
$(10,0)$
7.(树德实验)如图,等边三角形$ABC的顶点A(1,1)$,$B(3,1)$,规定把等边三角形$ABC先沿x$轴翻折,再向左平移$1$个单位长度为一次变换,如果这样连续经过$2016$次变换后,等边三角形$ABC中顶点C$的坐标为______.
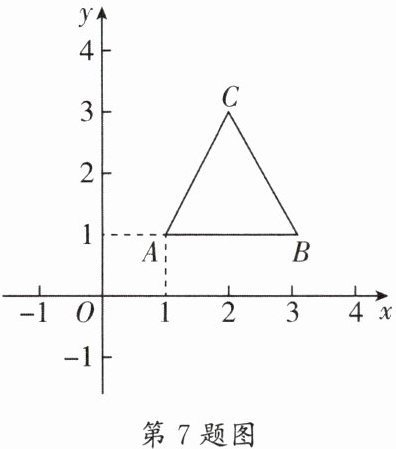

(-2014,√3+1)
答案:
解:
∵△ABC是等边三角形,A(1,1),B(3,1),
∴AB=3-1=2,AB中点横坐标为(1+3)/2=2,
点C到AB的距离为2×(√3/2)=√3,
∵AB在直线y=1上,且点C在AB上方,
∴点C的坐标为(2,1+√3)。
每次变换:沿x轴翻折后,点C纵坐标变为-(1+√3);向左平移1个单位,横坐标减1。
第二次变换:沿x轴翻折后,点C纵坐标变回1+√3;向左平移1个单位,横坐标再减1。
即每2次变换,纵坐标回到初始值1+√3,横坐标共减2。
2016次变换包含2016/2=1008个周期,
横坐标变化:2 - 2016×1= -2014,
纵坐标为1+√3,
∴经过2016次变换后,顶点C的坐标为(-2014,√3+1)。
答案:(-2014,√3+1)
∵△ABC是等边三角形,A(1,1),B(3,1),
∴AB=3-1=2,AB中点横坐标为(1+3)/2=2,
点C到AB的距离为2×(√3/2)=√3,
∵AB在直线y=1上,且点C在AB上方,
∴点C的坐标为(2,1+√3)。
每次变换:沿x轴翻折后,点C纵坐标变为-(1+√3);向左平移1个单位,横坐标减1。
第二次变换:沿x轴翻折后,点C纵坐标变回1+√3;向左平移1个单位,横坐标再减1。
即每2次变换,纵坐标回到初始值1+√3,横坐标共减2。
2016次变换包含2016/2=1008个周期,
横坐标变化:2 - 2016×1= -2014,
纵坐标为1+√3,
∴经过2016次变换后,顶点C的坐标为(-2014,√3+1)。
答案:(-2014,√3+1)
8.(实外)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中的“$\to$”方向排列,如$(1,0)$,$(2,0)$,$(2,1)$,$(3,2)$,$(3,1)$,$(3,0)$,…$$,根据这个规律探究可得,第$200$个点的坐标为______.
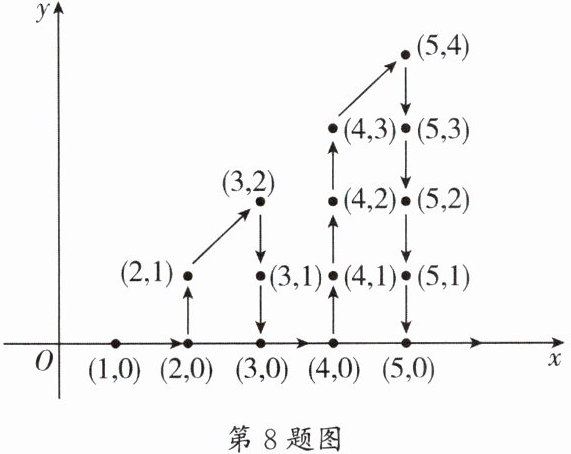

$(20,10)$
答案:
观察图形可知,每列点的个数依次为1,2,3,…,且偶数列点由下往上排列。
因为$1 + 2 + 3 + \cdots + 20 = \frac{20×(1 + 20)}{2} = 210$,
所以前20列共有210个点,第200个点是第20列从下往上数第$210 - 200 = 10$个点。
因此,第200个点的坐标为$(20, 10)$。
答案:$(20,10)$
因为$1 + 2 + 3 + \cdots + 20 = \frac{20×(1 + 20)}{2} = 210$,
所以前20列共有210个点,第200个点是第20列从下往上数第$210 - 200 = 10$个点。
因此,第200个点的坐标为$(20, 10)$。
答案:$(20,10)$
1. (西川)如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是 (
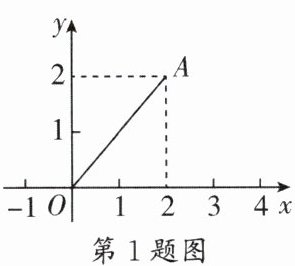
A.(2,0)
B.(4,0)
C.(-2√{2},0)
D.(3,0)
D
)
A.(2,0)
B.(4,0)
C.(-2√{2},0)
D.(3,0)
答案:
D[解析]如图,点A的坐标是(2,2),根据勾股定理可得OA=2$\sqrt{2}$,①若AP=PO,则P(2,0);②若AO=AP,则P(4,0);③若AO=OP,则P(2$\sqrt{2}$,0)或(−2$\sqrt{2}$,0).故点P的坐标不可能是(3,0).
2. (实外西区)如图,平面直角坐标系中有两点A(0,2),B(2√{3},0),在坐标轴上找一点P,使△PAB是等腰三角形.
(1)请问有几个这样的点P?
(2)这样的点P的坐标分别为
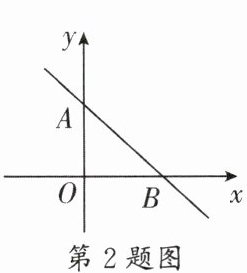
(1)请问有几个这样的点P?
6个
.(2)这样的点P的坐标分别为
(-2√3,0),(4+2√3,0),(-4+2√3,0),(2√3/3,0),(0,-2),(0,6)
.
答案:
(1)6个
(2)
- 当点P在x轴上时:
以AB为腰,PA=AB,计算得P(-2√3,0);
以AB为腰,PB=AB,计算得P(4+2√3,0);
以AB为底边,PA=PB,计算得P(-4+2√3,0);
以AB为腰,PA=AB,计算得P(2√3/3,0)。
- 当点P在y轴上时:
以AB为腰,PA=AB,计算得P(0,-2);
以AB为腰,PB=AB,计算得P(0,6)。
坐标分别为:(-2√3,0),(4+2√3,0),(-4+2√3,0),(2√3/3,0),(0,-2),(0,6)
(1)6个
(2)
- 当点P在x轴上时:
以AB为腰,PA=AB,计算得P(-2√3,0);
以AB为腰,PB=AB,计算得P(4+2√3,0);
以AB为底边,PA=PB,计算得P(-4+2√3,0);
以AB为腰,PA=AB,计算得P(2√3/3,0)。
- 当点P在y轴上时:
以AB为腰,PA=AB,计算得P(0,-2);
以AB为腰,PB=AB,计算得P(0,6)。
坐标分别为:(-2√3,0),(4+2√3,0),(-4+2√3,0),(2√3/3,0),(0,-2),(0,6)
查看更多完整答案,请扫码查看


