《2025年名校题库八年级数学上册北师大版》

1. (七中高新)构图法是解决数学问题的一种常见的方法. 比如:在$\triangle ABC$中,$AB$,$BC$,$AC三边的长分别为\sqrt {5}$,$\sqrt {10}$,$\sqrt {13}$,求这个三角形的面积. 如图,可以先建立一个正方形网格(每个小正方形的边长为 1),再在网格中画出格点$\triangle ABC$(即$\triangle ABC$三个顶点都在小正方形的顶点处),这样不需要求$\triangle ABC$的高,借用网格就能计算出它的面积. 试运用构图法求$\sqrt {m^{2}+2m+2}+\sqrt {m^{2}-6m+34}$的最小值,其值为______.

答案：
$2\sqrt {13}$ 【解析】$\because \sqrt {m^{2}+2m+2}+\sqrt {m^{2}-6m+34}=\sqrt {(m+1)^{2}+1}+\sqrt {(m-3)^{2}+25}=\sqrt {(m+1)^{2}+1}+\sqrt {(3-m)^{2}+25}$，$\therefore$ 可构造两直角边为 $m+1$ 和 $1$ 的 $Rt\triangle ACP$，两直角边为 $3-m$ 和 $5$ 的 $Rt\triangle BDP$，点 $P$ 在线段 $CD$ 上，则 $AP=\sqrt {(m+1)^{2}+1}$，$BP=\sqrt {(3-m)^{2}+25}$。如图，连接 $AB$，则 $\sqrt {(m+1)^{2}+1}+\sqrt {(3-m)^{2}+25}=AP+BP\geqslant AB$，即 $\sqrt {(m+1)^{2}+1}+\sqrt {(3-m)^{2}+25}$ 的最小值是线段 $AB$ 的长，过点 $B$ 作 $BE\perp AC$，交 $AC$ 的延长线于点 $E$，则四边形 $BDCE$ 是矩形，$\therefore CE=BD=5$，$BE=CD=m+1+3-m=4$。在 $Rt\triangle ABE$ 中，$AE=AC+CE=1+5=6$，由勾股定理，得 $AB=\sqrt {AE^{2}+BE^{2}}=\sqrt {6^{2}+4^{2}}=2\sqrt {13}$，$\therefore \sqrt {(m+1)^{2}+1}+\sqrt {(3-m)^{2}+25}$ 的最小值为 $2\sqrt {13}$。

2. (树德实验)如图,河边有$A$,$B$两个村庄,$A$村距河边 10 m,$B$村距河边 30 m,两村平行于河边方向的水平距离为 30 m,现要在河边建一抽水站$E$,需铺设管道抽水到$A村和B$村.
(1)要使铺设管道的长度最短,请作图找出抽水站$E$的位置(不写作法);
(2)若铺设管道每米需要 500 元,则最低费用为多少元?

答案：
解：
(1)如图，点 $E$ 即为所求点。

(2)如图，过点 $A'$ 作 $A'C\perp BC$ 于点 $C$，则 $A'C=30m$，$BC=40m$，$\therefore A'B=50m$，$\therefore$ 最低费用为 $50× 500=25000$（元）。

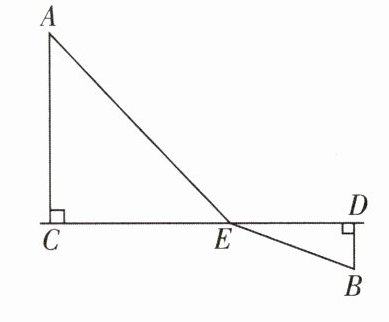
3. (实外)如图,$A$,$B$两个工厂位于一段直线形河的异侧,$A厂到河边的距离AC = 5\mathrm{km}$,$B厂到河边的距离BD = 1\mathrm{km}$,经测量$CD = 8\mathrm{km}$,现准备在河边某处(河宽不计)修一个污水处理厂$E$.
(1)设$ED = x\mathrm{km}$,请用含$x的代数式表示AE + BE$的长.
(2)为了使两厂的排污管道最短,污水处理厂$E$的位置应怎样来确定? 此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想$\sqrt {x^{2}+4}+\sqrt {(12 - x)^{2}+9}$的最小值为______.

答案：
解：
(1)$AE+BE=(\sqrt {5^{2}+(8-x)^{2}}+\sqrt {1^{2}+x^{2}})km$。
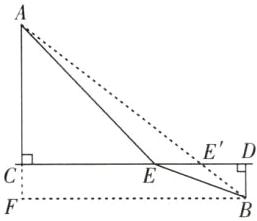
(2)如图，连接 $AB$ 交 $CD$ 于点 $E'$，点 $E'$ 即管道最短时污水处理厂的位置，过点 $B$ 作 $BF\perp AC$ 交 $AC$ 的延长线于点 $F$，易得 $AF=6km$，$BF=8km$，$\therefore AB=10km$，$\therefore$ 需要管道 $10km$。

(3)13