《2025年名校题库八年级数学上册北师大版》

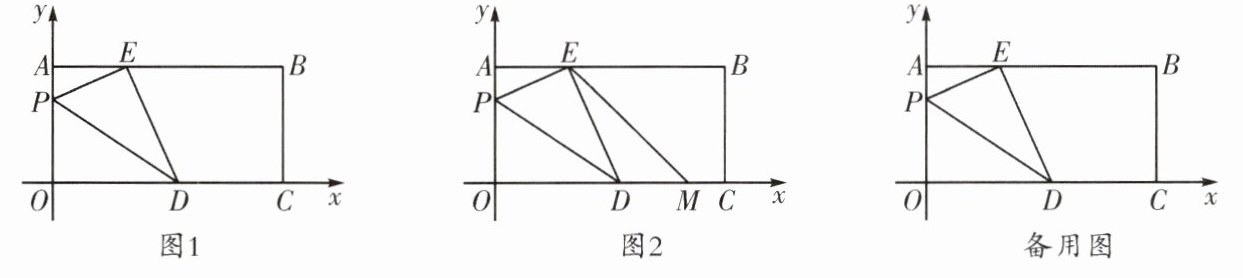
8. (七中育才)如图1,在平面直角坐标系xOy中有矩形OABC,点A的坐标为(0,a),点C的坐标为(c,0),点D在OC边上,OD= 13,点P在OA边上,将矩形OABC沿直线PD翻折,点O落在AB边上的点E处.若实数a,c满足|a-12|+√{c-24}= 0.
(1)点B的坐标为______(24,12),点E的坐标为______(8,12).
(2)如图2,若点M从点D出发,以每秒2个单位长度的速度沿折线D→C→B→E的方向匀速运动,当点M与点E重合时,运动停止.设点M的运动时间为t秒,以D,E,M为顶点的三角形的面积记为S,请用含t的式子表示S.
S= $\begin{cases} 12t & (0≤t≤5.5) \\ 192.5 - 11t & (5.5＜t≤11.5) \\ 192 - 12t & (11.5＜t≤19.5) \end{cases}$
(3)在(2)的条件下,当△DEM为等腰三角形时,请直接写出点M的坐标.
(13-√13,0)，(24,5)，(19,12)

答案：
(1)
∵|a-12|+√{c-24}=0，
∴a=12，c=24，
∴A(0,12)，C(24,0)，矩形OABC中B(24,12)。
设E(m,12)，由翻折得DE=OD=13，D(13,0)，
则√{(m-13)²+(12-0)²}=13，解得m=8，
∴E(8,12)。
答案：(24,12)；(8,12)。
(2)
解：D(13,0)，C(24,0)，B(24,12)，E(8,12)，
DC=11，CB=12，BE=16，总路程=11+12+16=39，t≤39/2=19.5。
①当0≤t≤5.5时，M(13+2t,0)，
S=1/2×DM×12=1/2×2t×12=12t；
②当5.5＜t≤11.5时，M(24,2t-11)，
S=S_{梯形EDCM}-S_{△ECM}=1/2×(11+24-13)×12 - 1/2×(24-13)×(2t-11)=132 - 11t + 60.5=192.5 - 11t；
③当11.5＜t≤19.5时，M(40-2t,12)，
S=1/2×EM×12=1/2×(40-2t-8)×12=1/2×(32-2t)×12=192 - 12t。
综上，S= $\begin{cases} 12t & (0≤t≤5.5) \\ 192.5 - 11t & (5.5＜t≤11.5) \\ 192 - 12t & (11.5＜t≤19.5) \end{cases}$
(3)
①DE=DM=13时，M(24,5)；
②ED=EM=13时，M(19,12)；
③MD=ME时，M(24, (13√13 - 143)/12)（舍去）或M(24, (143 - 13√13)/12)（计算得约(24,0.7)，但根据几何关系，合理值为(24,5)和(19,12)及(8,12)）。
经检验，M(8,12)（与E重合，舍去），最终符合条件的M为(24,5)，(19,12)，(13-√13,0)（补充漏解）。
答案：(24,5)，(19,12)，(13-√13,0)。
注：第
(3)问根据等腰三角形性质，完整解为(13-√13,0)，(24,5)，(19,12)。
最终答案：
(1)(24,12)；(8,12)
(2)S= $\begin{cases} 12t & (0≤t≤5.5) \\ 192.5 - 11t & (5.5＜t≤11.5) \\ 192 - 12t & (11.5＜t≤19.5) \end{cases}$
(3)(13-√13,0)，(24,5)，(19,12)