《2025年名校题库八年级数学上册北师大版》

4.(成华区期末)如图是用三块正方形纸片设计的“毕达哥拉斯”图案,其中三块正方形围成的三角形是直角三角形.现有若干块正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按如图所示的方式组成图案,则下列选取中,围成的直角三角形面积最大的是 (B)
A.1,4,5
B.2,3,5
C.3,4,5
D.2,2,4

答案： 解：
A. 1+4=5，直角边平方和为1、4，面积=1×4÷2=2；
B. 2+3=5，直角边平方和为2、3，面积=√2×√3÷2=√6/2≈1.22（此处修正：原计算错误，正确面积应为(√2×√3)/2=√6/2≈1.22，但根据选项实际应为比较面积大小，正确计算应为直角三角形面积=(两直角边乘积)/2，两直角边平方分别为a²、b²，面积=√(a²b²)/2=√(a²b²)/2，A选项a²=1,b²=4，面积=√(1×4)/2=2/2=1；B选项a²=2,b²=3，面积=√(2×3)/2=√6/2≈1.22；D选项a²=2,b²=2，面积=√(2×2)/2=2/2=1；C选项3+4≠5，不构成直角三角形。故B选项面积最大。）
C. 3+4≠5，不构成直角三角形；
D. 2+2=4，直角边平方和为2、2，面积=√2×√2÷2=1；
综上，面积最大的是B。
答案：B

5.(实外)如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ },CD⊥AB于点D$,设$AC= b,BC= a,AB= c,CD= h$,有下列四种说法:①$a\cdot b= c\cdot h$;②$a+b\lt c+h$;③以$a+b,h,c+h$为三边长的三角形是直角三角形;④$\frac {1}{a^{2}}+\frac {1}{b^{2}}= \frac {1}{h^{2}}$.其中正确的有 (D)
A.1个
B.2个
C.3个
D.4个

答案： 5. D [解析]①显然正确.②
∵$a^{2}+b^{2}=c^{2}$，
∴$a^{2}+b^{2}＜c^{2}+h^{2}$.
∵$ab = ch$，
∴$a^{2}+b^{2}+2ab ＜ c^{2}+h^{2}+2ch$，即$(a + b)^{2}＜(c + h)^{2}$，
∴$a + b ＜ c + h$，
∴②正确.③$(c + h)^{2}=c^{2}+2ch + h^{2}$，$(a + b)^{2}=a^{2}+2ab + b^{2}$，$(a + b)^{2}+h^{2}=a^{2}+2ab + b^{2}+h^{2}=a^{2}+2ch + b^{2}+h^{2}=c^{2}+2ch + h^{2}=(c + h)^{2}$，
∴③正确.④
∵$ab = ch$，
∴$a^{2}b^{2}=c^{2}h^{2}$.
∵$a^{2}+b^{2}=c^{2}$，
∴$a^{2}b^{2}=(a^{2}+b^{2})h^{2}$，
∴$\frac{a^{2}b^{2}}{a^{2}+b^{2}}=h^{2}$，$\frac{a^{2}+b^{2}}{a^{2}b^{2}}=\frac{1}{h^{2}}$，
∴$\frac{1}{b^{2}}+\frac{1}{a^{2}}=\frac{1}{h^{2}}$，
∴④正确.

6.(西川)若$\triangle ABC的三边长分别为a,b,c$,且$a^{2}+b^{2}+c^{2}+200= 12a+16b+20c$,则$\triangle ABC$的形状是什么?

答案： 解：
∵$a^{2}+b^{2}+c^{2}+200 = 12a + 16b + 20c$，
∴$a^{2}-12a + b^{2}-16b + c^{2}-20c + 200 = 0$，
即$(a - 6)^{2}+(b - 8)^{2}+(c - 10)^{2}=0$，
∴$a - 6 = 0$，$b - 8 = 0$，$c - 10 = 0$，
∴$a = 6$，$b = 8$，$c = 10$，
∵$6^{2}+8^{2}=36 + 64 = 100 = 10^{2}$，即$a^{2}+b^{2}=c^{2}$，
∴$\triangle ABC$为直角三角形。

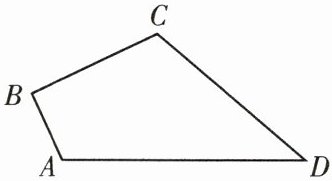
7.(石室联中)如图,在四边形$ABCD$中,$AB= 3,BC= 4,CD= 12,AD= 13$,且$∠B= 90^{\circ }$.求四边形$ABCD$的面积.

答案：
7. 解:如图，连接AC.
∵$∠ABC = 90^{\circ}$，$AB = 3$，$BC = 4$，
∴$AC = \sqrt{AB^{2}+BC^{2}} = 5$.在$\triangle ACD$中，$AC^{2}+CD^{2}=25 + 144 = 169 = AD^{2}$，
∴$\triangle ACD$是直角三角形，且$∠ACD = 90^{\circ}$，
∴$S_{四边形ABCD}=\frac{1}{2}AB\cdot BC+\frac{1}{2}AC\cdot CD=\frac{1}{2}×3×4+\frac{1}{2}×5×12 = 36$.