《2025年名校题库八年级数学上册北师大版》

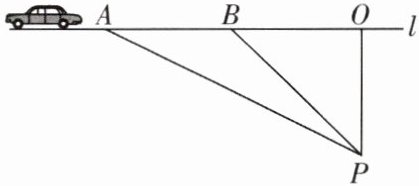
6. (青羊区期末)交通安全是社会关注的热点问题,安全隐患主要是超速和超载。某中学八年级数学活动小组的同学进行了测试汽车速度的试验。如图,先在笔直的公路l旁选取一点P,在公路l上确定点O,B,使得$PO⊥l,PO= 100$米,$∠PBO= 45^{\circ }$。这时,一辆轿车在公路l上由B处向A处匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得$∠APO= 60^{\circ }$。此路段限速每小时80千米,试判断此车是否超速? 请说明理由。(参考数据：$\sqrt {2}\approx 1.41,\sqrt {3}\approx 1.73$)

答案： 解：此车超速。理由如下：
∵PO⊥l，
∴∠POB=∠POA=90°。
∵∠PBO=45°，
∴△POB是等腰直角三角形，
∴OB=OP=100米。
∵∠APO=60°，
∴在Rt△APO中，tan∠APO=$\frac{OA}{OP}$，
即tan60°=$\frac{OA}{100}$，
∴OA=100·tan60°=100$\sqrt{3}$≈100×1.73=173米。
∴AB=OA-OB≈173-100=73米。
∴轿车速度v=$\frac{AB}{t}$=$\frac{73}{3}$米/秒。
∵$\frac{73}{3}$米/秒=$\frac{73}{3}$×3.6千米/时=87.6千米/时。
∵87.6千米/时＞80千米/时，
∴此车超速。

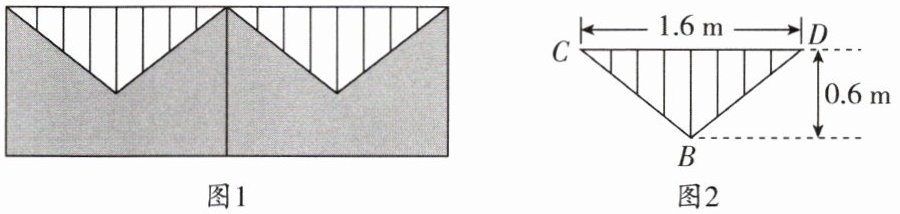
7. (锦江区期末)如图1所示的是围墙的一部分,上部分是由不锈钢钢管焊成的等腰三角形栅栏(如图2),请你根据图2所标注的尺寸,求焊成一个等腰三角形栅栏外框BCD至少需要不锈钢钢管多少米(焊接部分忽略不计)。

答案：
解：由题意，得BO⊥CD.
∵△BCD是等腰三角形，
∴$DO = \frac{1}{2}CD = 0.8$m.在Rt△BDO中，BD = $\sqrt{0.8^2 + 0.6^2} = 1$(m)，
∴BC = 1m，
∴焊成一个等腰三角形栅栏外框BCD至少需要不锈钢管1 + 1 + 1.6 = 3.6(m).

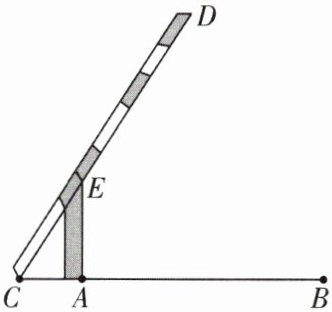
8. (双流区期末)如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口的宽AB为3.3m,在入口的一侧安装了停止杆CD,其中AE为支架。当停止杆仰起并与地面成$60^{\circ }$角时,停止杆的端点C恰好与地面接触,此时CA为0.7m。在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗? 请你通过计算说明。(参考数据：$\sqrt {3}\approx 1.7$)

答案：
解：不能.理由如下：在A，B之间找一点F，使BF = 2.5m.如图，过点F作GF⊥AB交CD于点G.
∵AB = 3.3m，AC = 0.7m，BF = 2.5m，
∴CF = 3.3 - 2.5 + 0.7 = 1.5(m).
∵∠DCA = 60°，∠GFC = 90°，
∴∠CGF = 30°，
∴CG = 2CF = 3m，
∴$GF = \sqrt{CG^2 - CF^2} = \frac{3\sqrt{3}}{2} \approx 1.7×1.5 = 2.55$(m) ＜ 3(m)，
∴这辆货车在不碰杆的情况下不能从入口内通过.