《2025年名校题库八年级数学上册北师大版》

3. (金牛区期末)如图,点A的坐标为(0,8),点B的坐标为(6,0),在x轴上确定一点P,使△PAB为一个等腰三角形,则点P的坐标可以是$\left(-\frac{7}{3},0\right)$或$(-6,0)$或$(16,0)$或$(-4,0)$.

答案： 解：设点P的坐标为$(x,0)$。
已知点A(0,8)，点B(6,0)，则：
$OA=8$，$OB=6$，$AB=\sqrt{(6-0)^2+(0-8)^2}=10$。
情况一：PA=PB
$\sqrt{(x-0)^2+(0-8)^2}=\sqrt{(x-6)^2+(0-0)^2}$
$x^2 + 64 = (x - 6)^2$
$x^2 + 64 = x^2 - 12x + 36$
$12x = -28$
$x=-\frac{7}{3}$
$\therefore P\left(-\frac{7}{3},0\right)$
情况二：PA=AB
$\sqrt{(x-0)^2+(0-8)^2}=10$
$x^2 + 64 = 100$
$x^2=36$
$x=\pm6$
当$x=6$时，点P与点B重合，舍去；
$\therefore x=-6$，$P(-6,0)$
情况三：PB=AB
$\sqrt{(x-6)^2+(0-0)^2}=10$
$|x - 6|=10$
$x - 6 = 10$或$x - 6=-10$
$x=16$或$x=-4$
$\therefore P(16,0)$或$P(-4,0)$
综上，点P的坐标可以是$\left(-\frac{7}{3},0\right)$或$(-6,0)$或$(16,0)$或$(-4,0)$。

4. (师大一中)如图,在平面直角坐标系中,长方形OABC的顶点A,C的坐标分别为(20,0),(0,8),D是OA的中点,点P在BC边上运动,当△ODP是以10为腰长的等腰三角形时,点P的坐标为(6,8)或(4,8)或(16,8).

答案： 解：
∵ 长方形OABC中，A(20,0)，C(0,8)，D是OA中点，
∴ D(10,0)，设P(x,8)，其中0≤x≤20。
情况1：OD=OP=10
OD=10，OP=√(x²+8²)=10，
x²+64=100，x²=36，x=6或x=-6（舍），
∴ P(6,8)。
情况2：OD=DP=10
DP=√[(x-10)²+8²]=10，
(x-10)²+64=100，(x-10)²=36，
x-10=±6，x=16或x=4，
∴ P(4,8)或(16,8)。
综上，点P的坐标为(6,8)或(4,8)或(16,8)。
答案：(6,8)或(4,8)或(16,8)

5. (成外)如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是长方形,点A,B,C,D的坐标分别为(7,0),(7,4),(-4,4),(-4,0),点E在线段OA上,点E的坐标为(5,0),点P在BC边上运动,使△OPE为等腰三角形,则满足条件的点P的坐标为______.

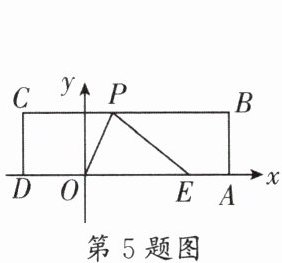
答案： 解：设点P坐标为(m,4)。
情况1：OP=OE。OE=5，OP²=m²+4²=25，解得m=±3。点P坐标(3,4)或(-3,4)。
情况2：OE=PE。PE²=(m-5)²+4²=25，解得m=2或m=8（8舍去）。点P坐标(2,4)。
情况3：OP=PE。m²+16=(m-5)²+16，解得m=2.5。点P坐标(2.5,4)。
综上，满足条件的点P坐标为(2.5,4)或(-3,4)或(3,4)或(2,4)。

6. (石室联中)如图,点A(1,0)在x轴上,点B(0,2)在y轴上,请问:在坐标轴上是否存在点P,使得△ABP是等腰三角形? 如果存在,请直接写出点P的坐标;如果不存在,请说明理由.

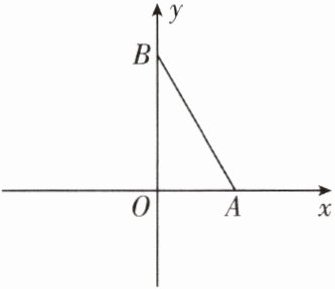
答案： 解：存在。
在x轴上：
- 以AB为腰，AP=AB时，AB=$\sqrt{(1-0)^2+(0-2)^2}=\sqrt{5}$，点P坐标为$(1+\sqrt{5},0)$或$(1-\sqrt{5},0)$；
- 以AB为腰，BP=AB时，点P坐标为$(-1,0)$；
- 以AB为底，PA=PB时，点P坐标为$\left(-\frac{3}{2},0\right)$。
在y轴上：
- 以AB为腰，BP=AB时，点P坐标为$(0,2+\sqrt{5})$或$(0,2-\sqrt{5})$；
- 以AB为腰，AP=AB时，点P坐标为$(0,-2)$；
- 以AB为底，PA=PB时，点P坐标为$\left(0,\frac{5}{4}\right)$。
综上，点P的坐标为$(1+\sqrt{5},0)$，$(1-\sqrt{5},0)$，$(-1,0)$，$\left(-\frac{3}{2},0\right)$，$(0,2+\sqrt{5})$，$(0,2-\sqrt{5})$，$(0,-2)$，$\left(0,\frac{5}{4}\right)$。

7. (七中育才)在平面直角坐标系中,已知点B(a,b),线段BA⊥y轴于点A,线段BC⊥x轴于点C,且$(a+2)^2+√{2a+b}= 0.(1)$求A,C两点的坐标;
(2)若D是BC的中点,E是线段OD上的一动点,记点E的横坐标为m,请用含m的代数式表示△AEC的面积;
(3)在(2)的条件下,当点E运动到OD的中点处时,请在y轴上确定一点P,使得△AEP为等腰三角形.(直接写出点P的坐标,不用书写过程)

答案： 解：
(1)
∵$(a + 2)^2+\sqrt{2a + b}=0$，$(a + 2)^2\geq0$，$\sqrt{2a + b}\geq0$
∴$a + 2 = 0$，$2a + b = 0$
解得$a=-2$，$b = 4$
∴点$B(-2,4)$
∵$BA\perp y$轴于点$A$
∴点$A$的坐标为$(0,4)$
∵$BC\perp x$轴于点$C$
∴点$C$的坐标为$(-2,0)$
(2)
∵$B(-2,4)$，$BC\perp x$轴于点$C$
∴点$C(-2,0)$，$BC$在直线$x=-2$上
∵$D$是$BC$的中点
∴点$D$的坐标为$(-2,2)$
设直线$OD$的解析式为$y = kx$
将$D(-2,2)$代入得$2=-2k$，解得$k=-1$
∴直线$OD$的解析式为$y=-x$
∵点$E$是线段$OD$上的一动点，点$E$的横坐标为$m$
∴点$E$的坐标为$(m,-m)$
过点$E$作$EF\perp y$轴于点$F$，则$EF = |m|$
∵点$E$在线段$OD$上，$O(0,0)$，$D(-2,2)$
∴$m$的取值范围是$-2\leq m\leq0$，则$EF=-m$
$A(0,4)$，$C(-2,0)$
$S_{\triangle AEC}=S_{\triangle AOC}-S_{\triangle AOE}-S_{\triangle COE}$
$S_{\triangle AOC}=\frac{1}{2}× OA×|x_C|=\frac{1}{2}×4×2 = 4$
$S_{\triangle AOE}=\frac{1}{2}× OA× EF=\frac{1}{2}×4×(-m)=-2m$
$S_{\triangle COE}=\frac{1}{2}×|x_C|×|y_E|=\frac{1}{2}×2×|-m|=|m|=-m$（$m\leq0$）
∴$S_{\triangle AEC}=4-(-2m)-(-m)=4 + 3m$
(3)$(0,4 + \sqrt{2})$，$(0,4-\sqrt{2})$，$(0,8)$，$(0,0)$